Una hormiga viajera
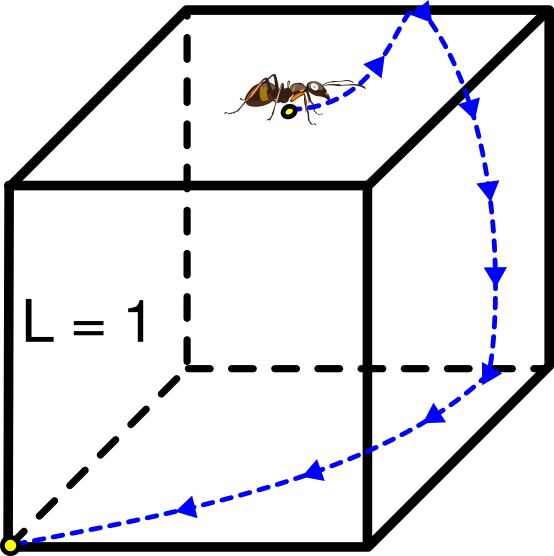
Una hormiga que está en el centro de la cara superior de un cubo quiere ir a un vértice de la cara inferior como se ve en la figura. Si la arista del cubo mide L = 1 ¿qué distancia mínima debe recorrer?
solución
Si nos imaginamos que el cubo es una caja ladeada en la que podemos abrir la tapa como se ve en la figura siguiente, la solución es inmediata ya que los puntos inicial y final de la hormiga ahora están en un plano y la distancia más corta entre ellos es el segmento que los une.
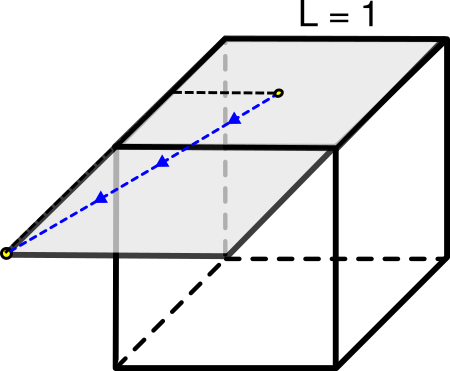
Con el teorema de Pitágoras:
Una serie infinita
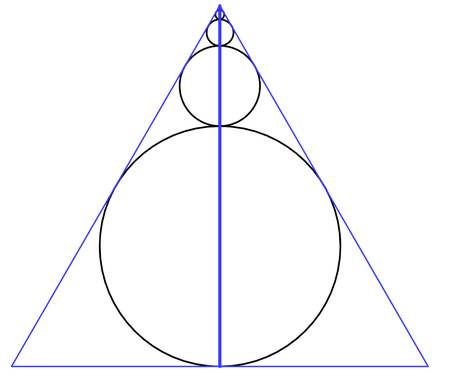
En un triángulo equilátero de lado L = 1 se inscribe una sucesión infinita de círculos, cada uno sobre el anterior, como se ve en la figura:
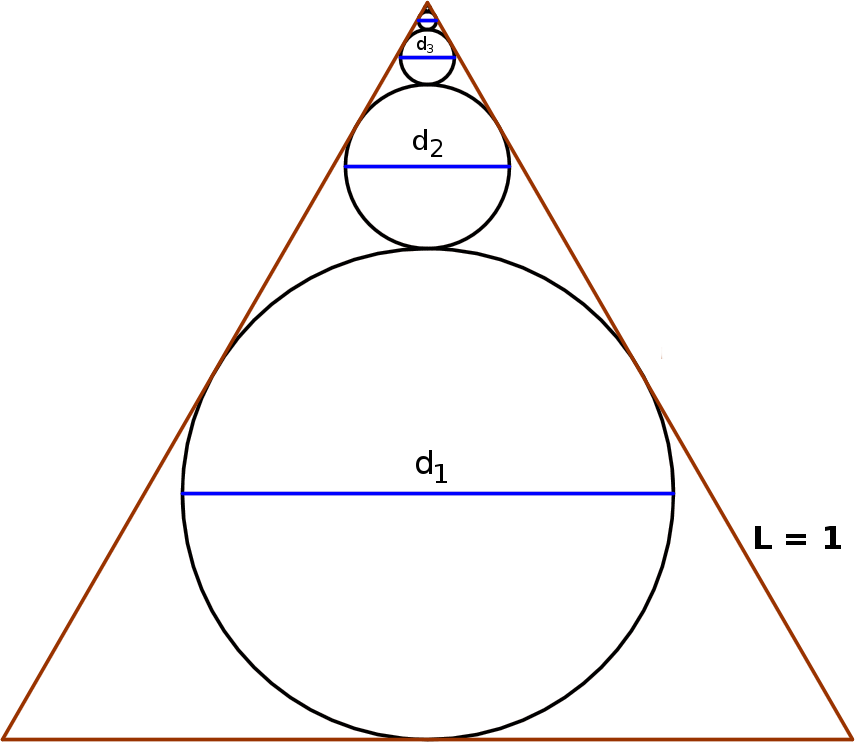
¿Cuanto vale la suma de los diámetros de todos los círculos?
solución
Si lo hacemos de la manera difícil:
El centro de un triángulo equilátero, y por tanto del círculo en él inscrito, está a una distancia de la base igual a 1/3 de la altura del triángulo. (Es fácil de comprobarlo mediante el teorema de Pitágoras)
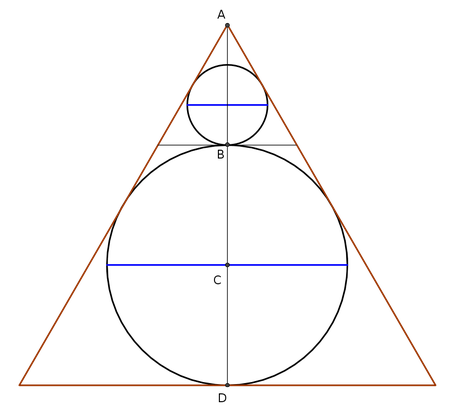
Si llamamos h a la altura, AD, el radio del primer círculo inscrito es 1/3 h y su diámetro:
La altura del segundo triángulo, AB, es 1/3 h y su diámetro por tanto:
Cada diámetro es entonces 1/3 del anterior y la suma de los diámetros:
Sacando factor común, 2/3 h:
en la entrada demostraciones sin palabras hemos visto que
La suma buscada de los diámetros es entonces
La forma inmediata de ver que la suma de los diámetros es la altura del triángulo es simplemente girar 90º los diámetros de los círculos inscritos:
y, ¿cuánto vale h?. De nuevo con el teorema de Pitágoras:
Geometría euclídea
En un cuadrante de circunferencia hay inscrito un rectángulo como se ve en la figura
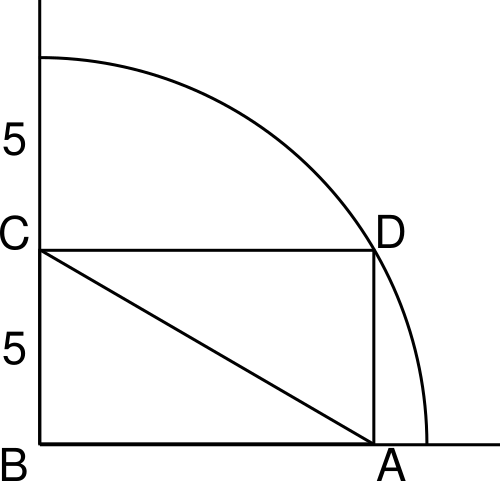
Determina la longitud de la diagonal AC
solución
La otra diagonal es el radio de la circunferencia: