Ajedrez y matemática recreativa

El ajedrez y las matemáticas recreativas tienen desde antiguo una muy buena relación. En la mayor parte de las recopilaciones de matemática recreativa aparecen curiosidades y problemas  que relacionan matemáticas y  ajedrez.
Muchos de lo grandes autores de matemática recreativa como Édouard Lucas, W. W. Rouse Ball, Henry Dudeney, Sam Loyd, Maurice Kraitchik o Martin Gardner, han tratado en sus obras cuestiones relacionados con el ajedrez.

Veamos a continuación algunos ejemplos que ilustran la gran variedad de problemas que se pueden plantear.

(ver soluciones)

El problema de las ocho damas

• Colocar sobre un tablero de ajedrez 8 damas de tal forma que no se amenacen entre si, o lo que es lo mismo que en cada fila, columna o diagonal haya como mucho una dama.
• ¿De cuántas maneras distintas se puede resolver el problema anterior?

Grandes matemáticos como Gauss o Cantor se han interesado por este problema  y sus generalización a n damas en tableros nxn.

El problema del caballo

• Recorrer con un caballo todo el tablero de ajedrez pasando una sola vez por cada casilla.
• ¿De cuántas maneras distintas se puede hacer el recorrido anterior?

Leonhard Euler en 1749 publicó un extenso estudio sobre este problema.

Henry Dudeney

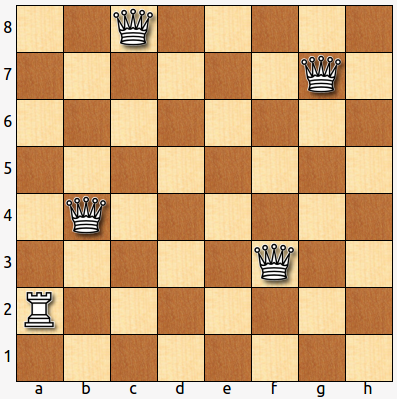
• Todas las casillas del tablero de la figura están  ocupadas o atacadas. El problema consiste en sustituir la torre por un alfil en la misma casilla, y luego situar las cuatro damas en otras casillas de tal manera que todas las casillas se encuentren de nuevo ocupadas o atacadas.

• Coloca ocho  alfiles (cuatro negros y cuatro blancos) en un tablero de ajedrez reducido, tal como se ve en la figura. El problema consiste en hacer que los alfiles negros intercambien sus posiciones con los blancos, ningún alfil debe atacar en ningún momento otro del color opuesto. Se deben alternar los movimientos, primero uno blanco, luego uno negro, luego uno blanco y así sucesivamente.
• ¿Cuál es el mínimo número de movimientos en que se puede conseguir?.

Sam Loyd

En su genial Cyclopedia podemos encontrar entre otros los dos siguientes:

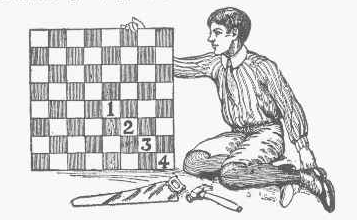
• Un muchacho recibió, como regalo, un tablero de ajedrez que había sido dividido en cuatro piezas de la misma forma y tamaño. Estaban numeradas respectivamente 1, 2, 3 y 4. El muchacho juntó las cuatro piezas formando el tablero que se ve en la figura. El problema consiste en revertir su trabajo, dividiendo el tablero en las cuatro piezas originales, iguales en forma y tamaño, de tal manera que cada una contenga uno de los números. [Pag 298]

• Loyd nos cuenta una anécdota de la historia francesa en la que el Delfín se salvo de un inminente mate cuando jugaba con el duque de Borgoña rompiéndole el tablero en la cabeza. En el dibujo se ven las ocho partes en que quedó dividido. El problema consiste en recomponer el tablero a partir de los 8 fragmentos. [pag. 97]

Ajedrez retrospectivo

En el ajedrez retrospectivo, también conocido como ajedrez retrógrado, se plantean problemas de lógica cuyo objetivo es determinar de que forma se ha alcanzado una determinada posición. No hace falta ser jugador de ajedrez solo es necesario conocer las reglas del juego. Raymond Smullyan ha escrito dos libros geniales sobre este tema: The Chess Mysteries of Sherlock Holmes y The Chess Mysteries of the Arabian Knights.
Los problemas que aparecen a continuación ilustran respectivamente las portadas de los mencionados libros.

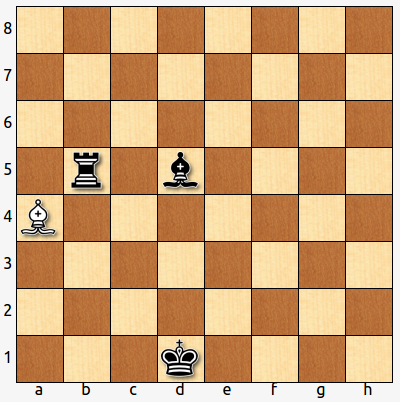
• Si el negro ha sido el último en mover, ¿cuál ha sido su movimiento? ¿y el último del blanco?

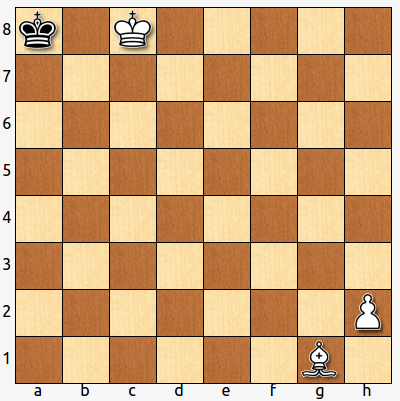
• El rey blanco se ha hecho invisible, ¿dónde está?

Otros Tipos

• ¿Cúantos cuadrados distintos se pueden construir utilizando como vértices las intersecciones de las líneas del tablero? ¿y rectángulos?

 

• ¿Cuántos posiciones distintas pueden formarse con las 32 piezas sobre el tablero?  Empezando con 2, luego 3 y así sucesivamente. (Para simplificar no tengamos en cuenta que muchas de ellas no se pueden dar si nos atenemos a las reglas del juego)

(ver soluciones a los problemas)

1. Bibliografía Específica

• Petković, Miodrag. 1997.  Mathematics and chess.  (Dover: New York)

100 problemas divididos en 6 apartados:

I Arithmetic andProbability.
II Chessboard Diversions.
III Chess-Piece Tours.
IV Geometric Puzzles.
V Mathematical Amusements and Games. VI Miscellaneous Puzzles.

Si hay que elegir un solo libro este sería un buen candidato.

• Frabetti, Carlo. 1995. El tablero mágico. Juegos y pasatiempos alrededor del ajedrez. (Gedisa: Barcelona)
  Catorce capítulos con los siguientes títulos:

  

  1. El ajedrez y los números
  2. Solos en el tablero
  3. El salto del caballo
  4. El problema de las ocho damas
  5. El humilde peón
  6. Alicia en el tablero de las maravillas
  7. Ajedrez heterodoxo
  8. Problemas atípicos
  9. Ajedrez retrógrado
  10. Tareas
  11. Metaproblemas
  12. El tablero roto
  13. El tablero usurpado
  14. El tablero inagotable

• Guik, Ye. Yá. 2012. Matemática en el Tablero de Ajedrez. (URSS: Moscú)
  Tres tomos:
  •  Tomo 1: El tablero y las piezas:

  

  1. 1. Matemática en los 64 escaques
     2.  El caballo camaleón
     3.  Problema del caballo
     4.  La poderosa dama
     5. Problema de las ocho damas
     6. La rectilínea torre
     7.  El perezoso rey
     8. El restringido alfil
     9. Independencia y dominación
     10. Valor de las piezas

• •  Tomo2.  Juegos matemáticos en el tablero de ajedrez:

• • 1. Récords matemáticos
    2. Problemas de permutación
    3. Juegos en tableros de formas inusuales
    4. Ajedrez cilíndrico
    5. Ajedrez hexagonal
    6. Ajedrez de fantasía
    7. Ajedrez de Fischer
    8. Juegos y problemas lógicos
    9. Geometría del tablero
    10. Simetría y asimetría
  • Tomo 3. La matemática de las puntuaciones y de los sistemas de torneos. Ajedrez computacional:

• 1. Viaje al pasado
  2. La matemática de los torneos
  3. Los cuadrados latinos y el ajedrez
  4. Puntuación de los Grandes Maestros
  5. Una excursión por la historia del ajedrez computacional
  6. La era de los nuevos campeones
  7. La hegemonía de las computadoras
  8. Campeonatos mundiales entre computadoras
  9. La computadora analiza
  10. Rompecabezas, problemas y estudios artísticos

•  Bonsdorff, E., Fabel, K., Riihimaa, O. 1974. Ajedrez y matemáticas. (Martínez Roca: Barcelona)
  Los capítulos en que se divide son

  

  1. :La apertura (Fabel)
  2. ¿Cuánto dura una partida de ajedrez? (Fabel)
  3. Partidas de mínima duración por mate (Bonsdorff)
  4. Series de movimientos con que empieza la partida (Bonsdorff)
  5. Series de movimientos de mínima longitud geométrica (Bonsdorff)
  6. El juego fortuito en el ajedrez (Bonsdorff).
  7. Análisis retroactivo (Bonsdorff)
  8. La posición inicial aparente (Bonsdorff)
  9. Ejercicios (Bonsdorff)
  10. El ajedrecista y la calculadora electrónica (Bandelow y Fabel)
  11. La movilidad de las piezas de ajedrez (Fabel)
  12. Los recorridos de las piezas de ajedrez (Fabel)
  13. Coordinaciones de piezas idénticas (Fabel).
  14. Coordinaciones de piezas diversas (Fabel)
  15. ¿Cuántas…? (Riihimaa)
  16. Partidas demostrativas breves (Riihimaa)
  17. Un poco de todo (Riihimaa)
  18. Las probabilidades (Fabel)
  19. Las valoraciones (Fabel)

• Watkins, John J.  2004. Across the Board. (Princeton University Press: Princeton)
  Subtitulado: The Mathematics of Chessboard Problems. Contiene los siguientes capítulos:

  

  1. Introduction
  2. Knights Tours
  3. The Knights Tour Problem
  4. Magic Squares
  5. The Torus and the Cylinder
  6. The Klein Bottle and Other Variations
  7. Domination
  8. Queens Domination
  9. Domination on Other Surfaces
  10. Independence
  11. Other Surfaces Other Variations
  12. Eulerian Squares
  13. Polyominoes

• Smullyan, Raymond. 1979. The Chess Mysteries of Sherlock Holmes. (Alfred A. Knopf: New York)
  Uno de los mejores libros para iniciarse en el apasionante mundo del retroanálisis.

• Smullyan, Raymond. 1981. The Chess Mysteries of the Arabian Knights. (Alfred A. Knopf: New York)

Hay edición en español:

• Smullyan, Raymond. 1987. Juegos y problemas de ajedrez para Sherlock Holmes. (Gedisa: Barcelona)

• Smullyan, Raymond. 1987. Juegos de ajedrez y los misteriosos caballos de Arabia. (Gedisa: Barcelona)

2. Otra Bibliografía

• Petković, Miodrag. 2009. Famous Puzzles of Great Mathematicians. (American Mathematical Society: Providence, Rhode Island)
  El capítulo décimo está dedicado al ajedrez e incluye un recorrido histórico por el problema del caballo y las 8 damas .
• Lucas, Edouard. Recreations Mathématiques. (Gauthier Villars: Paris) Cuatro volúmenes publicados entre 1891 y 1894
  Hace un estudio del problema de las 8 damas y trata también el recorrido del caballo.  Hay edición en español:
• Lucas, Edouard. Recreaciones Matemáticas. (Nivola: Madrid) Cuatro volúmenes publicados entre 2007 y 2008

• Kraitchik, Maurice. 1944. Mathematical Recreations. (George Allen:London)
  Dedica el capítulo décimo al problemas de las 8 damas. Hay edición en español:
• Kraitchik, Maurice.1946. Matemáticas Recreativas. (El ateneo: Buenos Aires)

• Borrel, Máximo. 1975. Ajedrez Brillante. (Bruguera: Barcelona)
  El capítulo quinto, El ajedrez y la ciencia y el décimo, pasatiempos basados en el ajedrez, contienen recreaciones y problemas matemáticos.
• Dudeney, Henry Ernest.  1917. Amusements in mathematics. (Nelson: London)
  Los problemas entre el 288 y el 361 están dedicados al ajedrez.
• Loyd, Sam. 1914. Cyclopedia of 5000 Puzzles, Tricks, and Conundrums with Answers. (Lamb: New York)
  Hay varios problemas relacionados con el ajedrez.

Martin Gardner escribió sobre recreaciones y problemas relacionadas con el ajedrez varias veces en su columna Mathematical Games que publicaba la revista Scientific American. Se pueden encontrar en los libros que las recopilan:

• Gardner, Martin. 1969. The unexpected hanging and other mathematical diversions. (Simon and Schuster: New York). Capítulo 16: The Eight Queens and Other Chessboard Diversions.
• Gardner, Martin. 1979. Mathematical Circus. (Knopf: NewYork). Capítulo 11: Eccentric Chess and other problems.
• Gardner, Martin. 1983. Wheels, Life and other Mathematical Amusements. (Freeman:New York). Capítulo 17: Chess Tasks.
• Gardner, Martin. 1991. Fractal Music, Hypercards and more…(Freeman:New York). Capítulo 15: Mathematical Chess Problems.

Hay edición española de los tres primeros:

• Gardner, Martin. 1991. El ahorcamiento inesperado y otros entretenimientos matemáticos. (Alianza Editorial: Madrid)
• Gardner, Martin. 1995. Circo matemático. (Alianza Editorial: Madrid)
• Gardner, Martin. 1998.  Ruedas, Vida y otras diversiones matemáticas. (Labor: Barcelona)