En esta entrada se describen algunas posibles estrategias paras que un programa de ordenador haga de descifrador en el juego de Muertos y Heridos.
En la entrada anterior de la que esta es una continuación se describe el juego y se analizan dos estrategias para descifradores humanos.
Estrategias para Ordenadores
El juego Muertos y Heridos especialmente en su variante conocida como Mastermind ha dado lugar a mucha bibliografía en la que se describen estrategias para programas informáticos que sean eficientes, tanto en el número, máximo y promedio, de jugadas empleado para deducir la clave, como en los recursos informáticos, capacidad de cálculo o memoria, necesarios.
Andy Pepperdine[1] en The game of MOO describe 11 estrategias para la variante conocida como MOO , e indica para cada una de ellas el número promedio y máximo de preguntas necesarias para deducir la clave. MOO o Bulls and Cows es como Muertos y Heridos pero sin repetición de dígitos.
A continuación se analizan dos estrategias intuitivas y muy fáciles de implementar en especial la primera.
Estrategia Simple
Propuesta por Ehud Shapiro[2] en 1983, el único criterio para elegir una nueva pregunta es que ésta se encuentre entre las claves posibles en ese momento. Inicialmente, antes de hacer la primera pregunta, hay 10000 posibles claves, los números del 0000 al 9999. Como cada pregunta que se hace reduce ese número, es inevitable que en algún momento se acierte la clave.
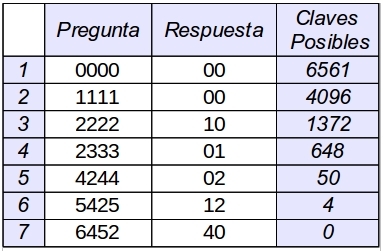
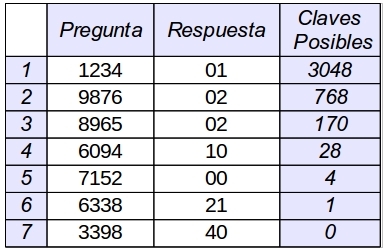
Las primeras preguntas suelen reducir en miles el número de claves posibles (Ver ejemplos en fig. 1 y fig. 2). En el caso más desfavorable el número de claves se reduce en una sola, la propia pregunta. (Ver fig. 3)
Una forma equivalente de plantear esta estrategia es decir que cada nueva pregunta tiene que ser compatible con las respuestas ya dadas a las preguntas anteriores, o lo que es lo mismo, si la nueva pregunta se supone que es la clave, las repuestas que obtendrían las preguntas anteriores serían las mismas que ya han obtenido en el juego.
En el ejemplo de la fig. 1, la clave que se escoge en cada momento es la menor de las posibles. El el ejemplo de la fig. 2 la la elección es aleatoria.


La estrategia funciona razonablemente bien en promedio aunque hay casos como el de la fig. 3 en los que dista mucho de ser óptima y pone en evidencia que hay situaciones en las que realizar preguntas que no sean posibles claves resulta mucho más eficiente. En la pregunta nº 3, si en lugar de 5880, que es una posible clave, se pregunta 2931, que no lo es, las claves posibles se reducen, en el caso más desfavorable, de 7 a 4.
Implementación de la Estrategia Simple
El script escrito en Python que está insertado a continuación implementa la Estrategia Simple. Se puede jugar contra ella o hacer que juegue contra si misma. En este caso sirve también como generador de problemas, solo hay que fijarse que la clave sea única cuando la respuesta es 40 .
En ambos casos tardará un poco en las primeras jugadas. El tiempo depende del ordenador en que se vea la página, ya que el script se ejecuta en el navegador.
Otras estrategias
Cada posible pregunta que se va a realizar divide al conjunto de claves posibles en 14 subconjuntos que se pueden identificar como: 40, 30, 22, 21, 20, 13, 12, 11, 10, 04, 03, 02, 01 y 00. En cada subconjunto se encuentran las claves que darían la misma respuesta a la posible pregunta. Algunos de estos conjuntos pueden estar vacíos en algún momento del juego.
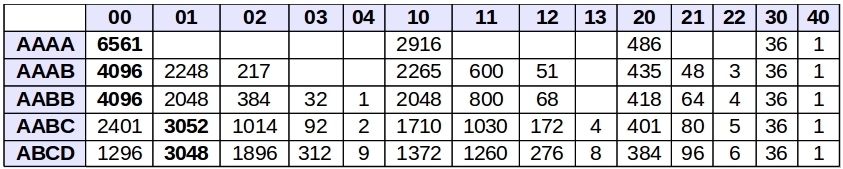
Inicialmente el conjunto de preguntas posibles es máximo, 10000, sin embargo muchas de ellas son equivalentes a los efectos de los mencionado en el párrafo anterior y podemos agruparlas según el número de dígitos repetidos en 5 grupos, ABCD, AABC, AABB, AAAB, AAAA. En la fig. 4 se muestra cuantos elementos tiene cada uno de los subconjuntos de la partición que en el conjunto de claves crea cada posible tipo de pregunta inicial.
MiniMax
A la vista de la tabla anterior podemos tratar de contestar a : ¿Qué forma debe tener la primera pregunta?. En negrita están marcados para cada tipo de pregunta las respuestas más desfavorables, entendiendo que son aquellas que dejan un mayor numero de claves posibles. Por ejemplo si hacemos una pregunta del tipo AAAA y obtenemos como respuesta 00, quedarían todavía 6561 claves posibles. Teniendo esto en cuenta parece razonable pensar que la pregunta debería ser aquella que haga que en el peor de los casos el numero de claves posibles sea mínimo. En la tabla anterior el mínimo de los máximos es 3048 y tiene lugar para una pregunta del tipo ABCD.
A partir de la segunda pregunta la creación de la tabla requiere un poco más de tiempo ya que no es tan inmediato clasificar las 1000 preguntas posibles como hacíamos en la primera.
Esta estrategia, usada en teoría de juegos, denominada MiniMax fue propuesta para el Mastermind por Donald Knuth[3] en 1976. No es de las mejores en cuanto al promedio de preguntas necesarias para deducir la clave pero si lo es en relación con el número máximo de preguntas.
En las figuras 5 y 6 se ven dos ejemplos de partidas en las que es descifrador utiliza la estrategia MiniMax. En ambos casos la clave no está pensada de antemano sino que cada respuesta que da el cifrador es la más desfavorable, compatible con las anteriores, esto es el Máximo de los Mínimos. [Salvo la primera en el segundo ejemplo]
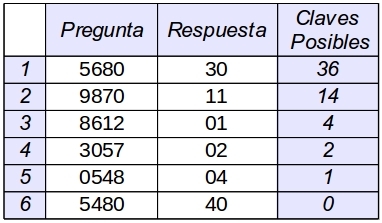
Los ejemplos anteriores están generados con un script en Python, que implementa el MiniMax. No he conseguido optimizarlo lo suficiente como para que se pueda ejecutar en esta entrada.
Otras Estrategias
Hay otras muchas estrategias en la bibliografía. Las dos que siguen dan muy buenos resultados:
- Estrategia de la máxima entropía. Esta estrategia propuesta por Neuwirth[4] se basa en la teoría de la información y trata de maximizar la información obtenida con cada pregunta.
- Estrategia de máximas particiones. Propuesta por Kooi[5] se basa en una idea muy simple, maximizar el número de particiones que cada posible pregunta crea en el conjunto de las claves posibles.
En el artículo de Kooi[5] se analizan todas las estrategias mencionadas.
El ordenador como cifrador
A la hora de probar estrategias, sobre todo para jugadores humanos resulta interesante utilizar al ordenador como cifrador, no clave «pensada» al inicio del juego, sino dando respuesta consistentes pero tratando de dar la mínima información posible. Una forma de hacerlo es escogiendo en cada momento el Mínimo del Máximo mencionado al hablar de la estrategia del MiniMax.
En el script que hay a continuación se puede jugar contra el ordenador, que actúa de cifrador, usando el sistema mencionado.
En las primeras preguntas tardará un poco dependiendo del ordenador en que se ejecute.
Bibliografía
[1] Pepperdine, Andy. 2007. The Game of MOO, http://www.pepsplace.org.uk/Trivia/Moo/Moo.pdf (2007)
[2] Shapiro, E. 1983. Playing Mastermind Logically. SIGART Newsletter , Vol. 85, pp. 28–29.
[3] Knuth, D.E. 1976. The computer as mastermind. J. Recreational Math.,Vol 9(1) pages 1–6.
[4] Neuwirth, E. 1982. Some Strategies for Mastermind. Zeitschrift f ̈ur Operations Research, Vol. 26, pp. 257-278.
[5] Kooi, B. 2005. Yet another mastermind strategy . ICGA Journal, 28 (1), pp. 13-20.

Un comentario en “Muertos y Heridos: Un juego de lógica (y II)”