¿Qué es resolver el cubo?
Resolver el Cubo de Rubik consiste en conseguir que cada una de sus caras tenga un único color.
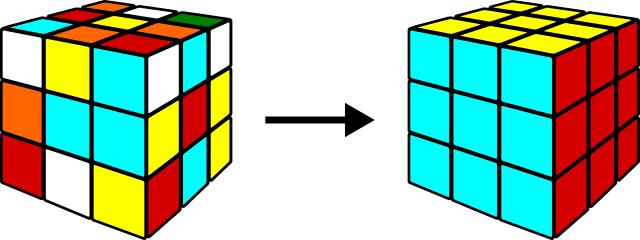
Hay dos manera muy distintas de afrontar esta tarea: como un ejercicio o como un problema.
Resolver el cubo como un ejercicio
Un ejercicio es una tarea de la que conocemos el objetivo y sabemos como alcanzarlo. Lo que se pretende al realizar el ejercicio es practicar herramientas ya conocidas que permiten alcanzar el objetivo.
Por ejemplo cuando aprendemos a sumar el maestro nos hará practicar la suma con ejercicios como el siguiente:
Suma todos los números del 1 al 10
En multitud de lugares en la web y en las redes sociales se enseña como resolver el cubo de esta manera. Se puede seguir un video, utilizar una aplicación, leer un manual. Hay métodos para principiantes, para hacerlo muy rápido, para hacerlo en pocos movimientos, …
En todos estos lugares se plantea la resolución del cubo como un ejercicio: estudiar , memorizar y practicar el método que se propone.
Resolver el cubo como un problema
Un problema es una tarea en la que conocemos el objetivo pero no sabemos, como alcanzarlo.
Siguiendo con el ejemplo de la suma, un profesor al cabo de unos años podría proponernos la siguiente suma como un problema:
Suma, en unos pocos minutos con lápiz y papel, los enteros del 1 al 1000000.
(Sería un problema si no hubiésemos estudiado todavía las herramientas que lo convierten en un ejercicio)
En muy pocos lugares dedicados al cubo se dice que resolver el cubo se puede intentar como un problema y si se hace, probablemente se disuada al osado diciendo que es una tarea extremadamente compleja al alcance de muy pocos.
El objetivo de esta entrada es convencer al lector de que resolver el cubo como un problema es posible y está al alcance de cualquiera que se lo proponga.
¿Por qué resolver el cubo de Rubik sin que nadie nos cuente como hacerlo?
Resolver el cubo sin ayuda externa requiere más tiempo, paciencia y perseverancia pero no solo será más satisfactorio, sino que mejorará más nuestra autoestima, memoria, concentración y capacidad para resolver problemas.
Además de todo lo dicho en el párrafo anterior hay una razón quizás más fundamental para hacerlo:
Resolver el cubo de Rubik sin ayuda es mucho más divertido
Ahora es un buen momento para dejar de leer e intentar resolver el cubo como un problema
¿Cómo resolver un problema?
Miguel de Guzmán Ozámiz fue un matemático español interesado, entre otras muchas cosas, en como resolver problemas. En varios de sus libros propone un método que adaptándolo a resolver el cubo como problema podría ser algo así:
- Familiarízate con el problema
- Entiende cual es el objetivo que buscas
- Familiarízate con el funcionamiento del cubo
- Juega libremente con él
- Optimiza la forma en que tus dedos hacen girar las caras
- Aprende a desmontarlo y montarlo en su forma ordenada
- Entiende como funciona internamente
- Busca estrategias
- Intenta pensar en distintas formas de atacar el problema. No importa que parezcan descabelladas
- Busca semejanzas con otros problemas que conozcas
- Empieza por otro problema parecido pero más sencillo
- Experimenta, busca regularidades o pautas
- Haz dibujos, esquemas. Representa tus ideas. Coloréalas
- Modifica el problema. Busca problemas parecidos
- Utiliza una notación adecuada para registrar tus progresos
- Aplica la estrategia
- Aplica las distintas estrategias anteriores
- Si una no funciona no la abandones a la primera pero tampoco te obceques con ella
- Revisa tu trabajo
- ¿Cómo has llegado a la solución?
- ¿Qué estrategia es la que ha funcionado mejor? ¿Por qué ha funcionado? ¿Puedes mejorarla?
- ¿Por qué no has llegado? ¿Has quedado a medias? ¿Puedes cambiar la estrategia?
- ¿Puedes usar el método utilizado en otros contextos?
- Reflexiona sobre todo el proceso
En estos libros de Miguel de Guzmán puedes encontrar más información sobre como resolver problemas:
Guzmán, M. de. 1994. Para pensar mejor. Pirámide.
Guzmán, M. de. 2003. Cómo hablar, demostrar y resolver en Matemáticas. Anaya Educación
El matemático húngaro George Polya publicó en 1945 un libro sobre el tema que se ha convertido en un clásico. Se sigue publicando en la actualidad:
Polya, G. 1945. How to Solve It: A New Aspect of Mathematical Method. Princeton University Press
Hay edición el español:
Polya, G. 1965. Cómo plantear y resolver problemas. Editorial Trillas.
Ahora es un buen momento para dejar de leer e intentar resolver el cubo como un problema
Resolver el cubo como un problema
La elaboración y aplicación de un método de resolución de problemas como el presentado es algo personal. A continuación se muestran ejemplos de como podrían ser el desarrollo de alguna de las etapas del método propuesto para resolver el cubo como un problema.
Hacerse con un cubo
Ayuda tener un par de cubos para practicar. No hace falta gastarse mucho dinero. Un cubo magnético de una buen fabricante como el Moyu Meilong 3 M 2020 se puede comprar al día de escribir esto por 8,50 € en Juegos Besa.
Jugar libremente
Familiarízate con el cubo jugando libremente con él. Optimiza la forma de mover cada una de sus caras y capas.
Montar, desmontar y limpiar el cubo
Poder desmontar y volverlo a montar permite volver el cubo a su posición ordenada antes de saber resolverlo.
Estructura. Terminología. Notación
Se describe el cubo, su funcionamiento, una terminología y una notación para registrar los avances en su resolución.
Partes del cubo
Un Cubo de Rubik es, aparentemente, un conjunto de 27 cubitos apilados en tres capas de 9 cubitos cada una. El cubito central, que no se ve, realmente no existe.

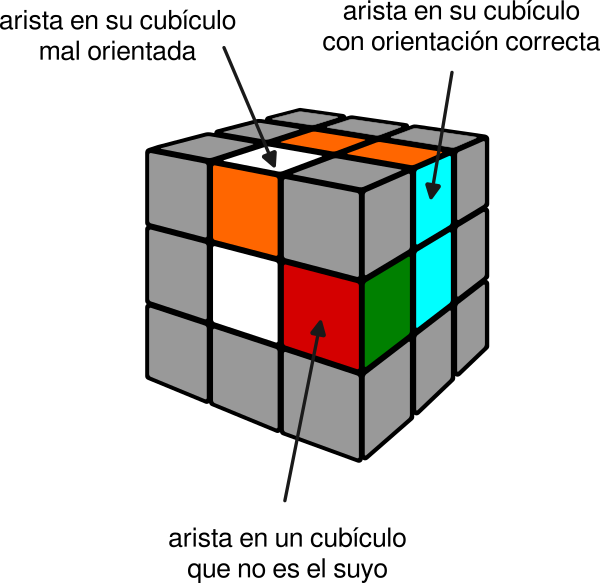
Los 26 cubitos que se ven se pueden clasificar según el número de sus caras visibles:
Centros (6): una sola cara visible.
Aristas (12): dos caras visibles.
Vértices (8): tres caras visibles.
Cada cara puede girar, en torno a su centro, de forma independiente y en ambos sentidos, horario y antihorario. De las misma manera pueden girar las tres capas interiores: las dos verticales y la horizontal.
Los cubitos que están en el centro de cada cara definen el color de la misma ya que su posición, relativa a los otros centros, no cambia cuando las caras o capas giran.
Un cubículo es el hueco en el cubo donde se aloja un cubito.
Una cubo arista admite dos orientaciones diferentes. mientras que un cubo vértice tiene tres.

Se necesita una notación
El registrar lo que se hace, con una notación adecuada, permite organizar la información fácilmente.
A continuación se describe la notación estándar para transcribir los giros de las caras y capas que forman el cubo.
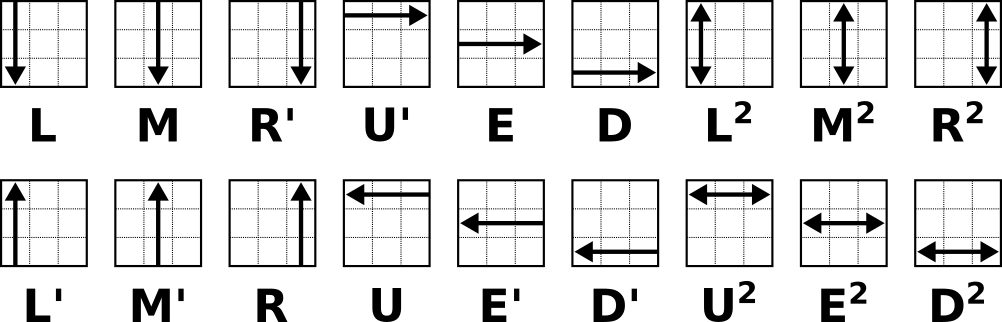
Los giros de las caras, 90º, en el sentido de las agujas del reloj según se mira a la cara, se representan por las letras U, D, R, L, F, B
| U (Up ) Arriba | 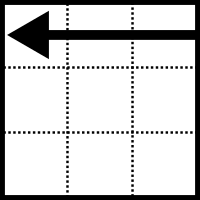 | L (Left) Izquierda | 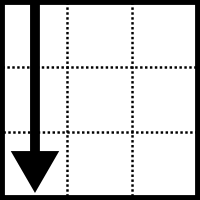 | F (Front ) Delante |  |
| D (Down) Abajo | 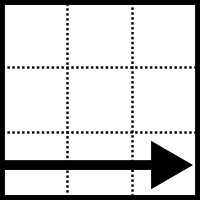 | R (Right) Derecha | 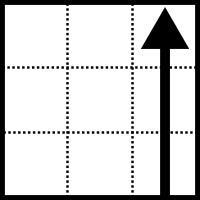 | B (Back) Atras |  |
Los giros de las caras, 90º, en el sentido contrario al de las agujas del reloj según se mira a la cara se representan por las mismas letras seguidas de un apóstrofe U’, D’, R’, L’, F’, B’
Los giros de las tres capas centrales del cubo se representan mediante las letras M, E, S
M (Midle = Media) : Capa entre izquierda y derecha. M representa un giro de 90º en el sentido de las agujas del reloj visto desde la izquierda.
E (Equator = Ecuador) : Capa entre arriba y abajo. E representa un giro de 90º en el sentido de las agujas del reloj visto desde abajo.
S (Standing = De pie): Capa entre delante y atrás. S representa un giro de 90º en el sentido de las agujas del reloj visto desde delante
Los giros de las caras 180º se pueden representar añadiendo un 2 a continuación de la letra o como exponente, U2, D2, R2, L2, F2, B2, M2, E2, S2 o U2, D2, R2, L2, F2, B2, M2, E2, S2
Alternativamente se pueden utilizar dibujos, más intuitivos pero también más engorrosos para transcribir. Por ejemplo:
Secuencia de movimientos
La realización de giros de capa uno a continuación de otros se denomina secuencia. A continuación dos ejemplos de secuencias: S1 = LDL’D’ , S2 = R2 D2
Para indicar la repetición de una secuencia se utilizan paréntesis y un exponente que indica el número de veces que hay que repetir el grupo. Por ejemplo: (R2 D2)3 equivale a R2 D2 R2 D2 R2 D2
Inversa de una secuencia
Cada movimiento de cara o capa puede deshacerse realizando su movimiento inverso a continuación. Por ej. el giro de una cara o capa en sentido horario se deshace girando a continuación la misma cara o capa en sentido antihorario. Así L se deshace con L’ y M’ se deshace con M. Cuando se quiere deshacer una secuencia de movimientos hay que realizar, en orden inverso, los movimientos inversos de cada uno de los que formaban la secuencia original. Este forma de proceder es la misma que seguiríamos si nos ponemos una camiseta, encima nos ponemos una camisa y nos anudamos la corbata, y a continuación queremos deshacerlo todo. Tendríamos que deshacer las tres acciones en orden inverso, primero deshacer el nudo, segundo quitar la camisa y por último quitar la camiseta.
Para deshacer S = L D L’ D L D2 L’ haríamos su inversa S-1 = L D2 L’ D’ L D’ L’
Más ideas para familiarizarse
Una entrada anterior está dedicada a ciertos aspectos matemáticos del cubo que pueden resultar de ayuda a la hora de intentar resolverlo. En la sección: Un buen lugar para comenzar hay ideas para familiarizarse con el cubo.
Ahora es un buen momento para dejar de leer e intentar resolver el cubo como un problema
Problemas parecidos pero más sencillos
Cubo resuelto
A la hora de intentar resolverlo, con frecuencia se toma un cubo revuelto como punto de partida. Un cubo ordenado puede ser un mejor punto de partida ya que al desordenarlo de forma controlada se puede obtener información valiosa.
Cubos especiales

Hay cubos 3x3x3 que tienen menos colores. A medida que el número de colores se reduce resolver el cubo se simplifica.
Utilizando pegatinas es fácil fabricar cubos con el número de colores que se desee.
Cubos 2x2x2

Un cubo 2x2x2 es un 3x3x3 al que se le han quitado: los cubitos arista, los centros de cara y el cubito central. Su resolución es más sencilla, solo cubitos vértice. Lo que se aprende al resolverlo es un buen punto de partida para atacar la resolución del 3x3x3.
Ejercicios sobre un 3x3x3
Los ejercicios que se proponen a continuación están ordenados según su creciente dificultad. Es fácil que no todo el mundo esté de acuerdo con el criterio. Al empezar cada ejercicio el cubo debe estar desordenado.
- Haz que en todas las caras del cubo aparezca el color rojo
- Haz que en todas las caras del cubo aparezcan los colores rojo y azul
- Haz que en una cara del cubo aparezcan los seis colores
- Sitúa los cuatro cubitos arista de la cara naranja en sus cubículos (No es necesario que estén bien orientados)
- Sitúa los cuatro cubitos arista de la cara naranja en sus cubículos con la orientación correcta.
- Sitúa los cuatro cubitos arista de la capa E (Capa entre arriba y abajo) en sus cubículos con la orientación correcta.
- Sitúa los cuatro cubitos vértice de la cara naranja en sus cubículos (No es necesario que estén bien orientados)
- Sitúa los cuatro cubitos vértice de la cara naranja en sus cubículos con la orientación correcta.
- Sitúa los cuatro cubitos arista y los cuatro cubitos vértice de la cara naranja en sus cubículos (No es necesario que estén orientados)
- Sitúa los cuatro cubitos arista y los cuatro cubitos vértice de la cara naranja en sus cubículos con la orientación correcta.
Ahora es el mejor momento para dejar de leer e intentar resolver el cubo sin más ayuda.
Cómo seguir
Una forma de sencilla de abordar la resolución del cubo es hacerlo capa a capa: superior, media e inferior.
La primera capa, el ejercicio 10 de la lista anterior, es una tarea asequible si se han hecho los 9 primeros ejercicios y se le ha dedicado un tiempo razonable.
Para ordenar las otras dos capas hacen falta secuencias de movimientos que cambien únicamente la orientación y/o posición de unos pocos cubitos.
¿Cómo encontrar secuencias interesantes que cambien la ubicación y/o orientación de unos pocos cubitos?
Una idea para la búsqueda es utilizar el hecho de que el orden en que se realizan los giros de las caras del cubo importa:
Si se realizan dos secuencias X e Y y a continuación se quiere deshacer lo hecho, hay que utilizar las inversas de X Y, en el orden inverso Y-1X-1,
XYY-1X-1
Sin embargo si las inversas se realizan en el orden original,
XYX-1Y-1
el cubo, normalmente, no retorna a su estado anterior sino que unos pocos cubitos cambian su orientación y/o ubicación.
Si la longitud de las secuencias no es muy grande los cambios tampoco lo serán.
Un ejemplo, S1
Si X = LDL’ e Y = E,
entonces X-1 = LD’L’ e Y-1 = E’,
la secuencia interesante que buscamos es S1= XYX-1 Y-1= (LDL’)E (LD’L’) E’
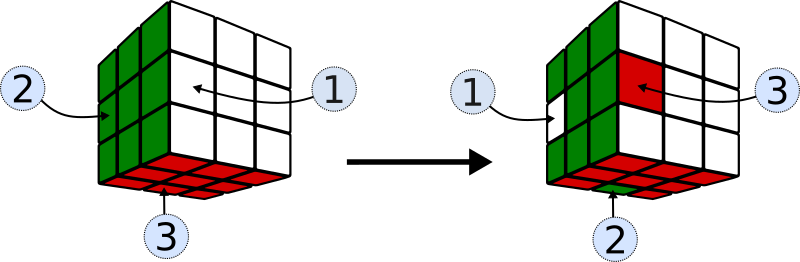
S1, produce únicamente el cambio de ubicación de tres cubitos arista.
Una vez localizada una secuencia interesante se puede utilizar como punto de partida para localizar otras relacionadas. A continuación tres nuevas secuencias a partir de S1
Una variación, S2
Variando Y ligeramente, por ejemplo Y = E²,
se obtiene una nueva secuencia S2 = XYX-1 Y-1= (LDL’)E²(LD’L’) E²,
que producirá, probablemente, cambios no muy diferentes de los que producía la secuencia original. En este caso afectan también a la ubicación de tres cubitos pero distintos a los de la secuencia original en la que Y = E.
Otra variación, S3
La secuencia S1 cambia la ubicación de 3 aristas en 2 capas distintas.
Tomado S1 como punto de partida es posible crear una secuencia que cambie la ubicación de 3 aristas de la misma capa de la siguiente manera.
S3= E S1E’
Esta es una idea interesante que se desarrolla un poco más abajo
Construir una secuencia (S4) a partir de otra (S1)
La secuencia S1 que cambiaba la ubicación de tres cubitos se puede utilizar para construir otra que solo cambia orientaciones.
S4 = S1 L2 S1 L2
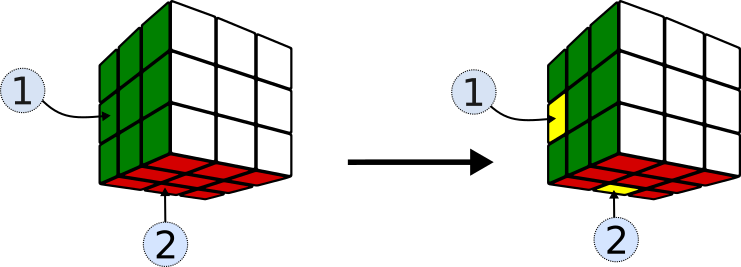
produce el único efecto de alterar la orientación de dos aristas.
Ejercicio: Analizar la construcción de S4
Utilizando S4 con otros fines
Tomando como base la secuencia, S4, que cambia la orientación de dos cubitos arista contiguos, C1 y C2, es posible cambiar la orientación de dos cubitos arista cualesquiera Cw y Cz. Para ello se sitúan Cw y Cz en posiciones contiguas, se cambian sus orientaciones con S4,y por último se devuelven Cw y Cz a sus posiciones originales deshaciendo los movimientos que los pusieron en posiciones contiguas.
Por ejemplo, para cambiar dos aristas opuestas de la capa central haríamos
(R’D) S4 (D’R)
(R’D) sitúa la segunda arista en la posición adecuada, S4 cambia la orientación de las dos y (D’R) devuelve la segunda arista a su posición original.
Esta forma de proceder nos da una herramienta con mucho potencial:
«A partir de una secuencia que realiza ciertos cambios sobre un grupo de n cubitos en cierta posición relativa, se puede construir otra que realice los mismos cambios sobre otro grupo de n cubitos en una posición relativa diferente.«
La segunda capa
Con las secuencias anteriores se pueden ubicar y orientar las aristas del cubo que forman la segunda capa
La tercera capa
Para resolver la tercera capa son necesarias nuevas secuencias que sitúen y orienten los vértices.
Ubicar vértices, S5 y S6
La siguiente secuencia,
S5 = (LR’D) (L’D’R)(DL)(D’L’)
mueve 3 vértices de la base cambiándoles también la orientación.
(Los paréntesis ayudan a entender y memorizar la secuencia ya que resaltan su estructura)
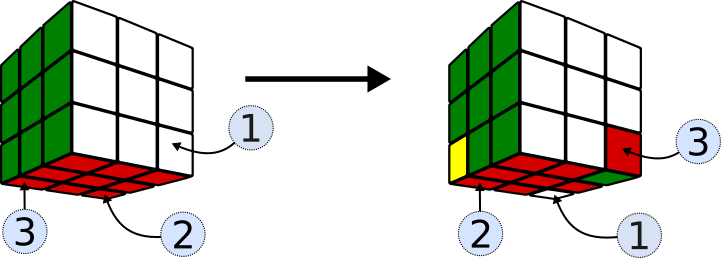
Si a S5 se le añade D’, se obtiene
S6 = S5 D’

Si nos olvidamos de lo que le sucede a las aristas de la base y a las orientaciones de los vértices, el efecto de S6 es intercambiar 2 vértices de la base
S6 es suficiente para ubicar los vértices de la base.
Orientar vértices, S7
Para orientar los vértices de la base una vez ubicados es suficiente la siguiente secuencia:
S7 = (R’D’)(RD’)(R’D)(DR)(LD)(L’D)(LD’)(D’L’)
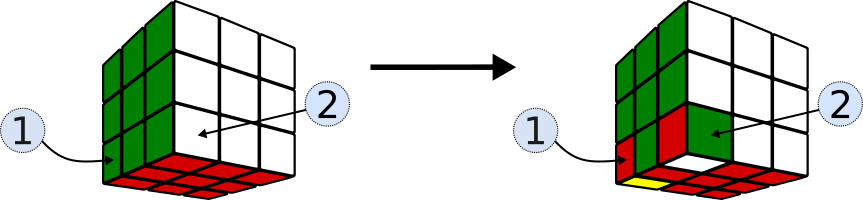
S7 hace girar dos vértices de la cara inferior. Como en todas las secuencias, su inversa,
S7‘ = (LD)(DL’)(D’L)(D’L’)(R’D’)(D’R)(DR’)(DR)
deshará el efecto de S7 haciendo girar los mismo vértices en sentido contrario.
Ejercicio: Las 4 primeras secuencias, S1, S2, S3 y S4, afectan a cubitos arista y las 3 últimas, S5, S6 y S7, a cubitos vértice. ¿Qué tienen en común unas y otras para que se comporten de esta manera?
Resolver el cubo
Aunque es posible resolver el cubo usando únicamente algunas de las secuencias vistas, es obvio que cuanto mayor sea la variedad de las que disponemos más sencillo y rápido será resolverlo.
Utilizando las ideas expuestas es fácil y divertido añadir otras secuencias a la caja de herramientas.
Una idea para empezar esa tarea es incorporar a la caja las secuencias inversas de las que ya tenemos. El poder usar una o la otra puede simplificar significativamente el tiempo de resolución.
Más problemas para continuar
Si ya has resuelto el cubo y te has quedado con ganas de más, aquí tienes una forma de que no se acabe la diversión:
Cuando se resuelve el cubo, sus caras centrales también giran aunque no se note. Este hecho se puede utilizar para estirar la diversión.
Orienta el cubo de una manera determinada según los colores de sus caras. Por ejemplo:
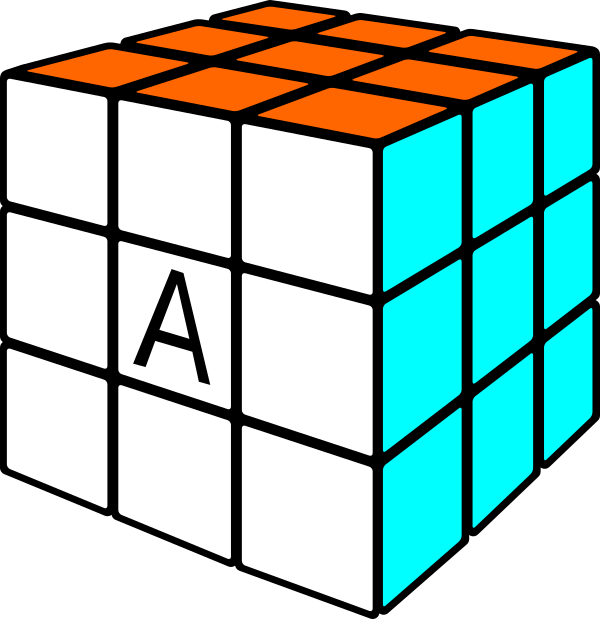
- izquierda:verde
- derecha: azul
- delante: blanco
- detrás: amarillo
- arriba: naranja
- debajo: rojo
Dibuja la letra «A» verticalmente en el cubito central de la cara blanca.
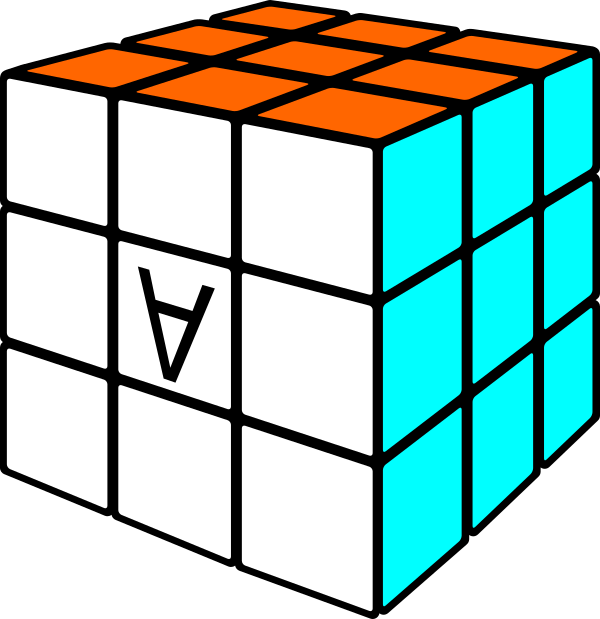
Problema 1: Conseguir que el cubito central de la cara blanca gire 180º de forma que la letra «A» se vea invertida, sin cambiar la orientación establecida del cubo
Problema 2: Lo mismo que el problema 1 pero con un giro de 90º
Es posible complicarlo más escribiendo letras u otros símbolos en todas las caras centrales. (Evidentemente no todos los símbolos sirven para este fin ya que su simetría puede hacer que los giros no se noten)

