Demostraciones sin palabras: soluciones

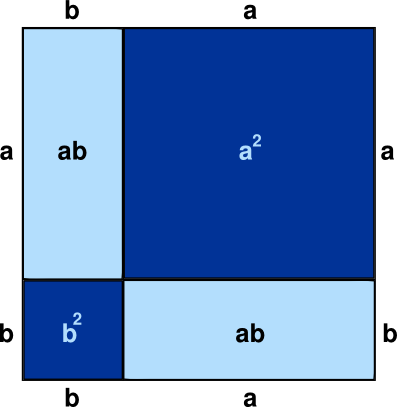
En las siguientes imágenes se visualizan relaciones matemáticas. Los matemáticos no se ponen de acuerdo si constituyen demostraciones formales con la misma validez que las convencionales con palabras. De lo que no hay duda es que fomentan el pensamiento matemático y permiten comprender y visualizar mucho mejor las relaciones que de ellas se deducen. En el enlace final están las soluciones.

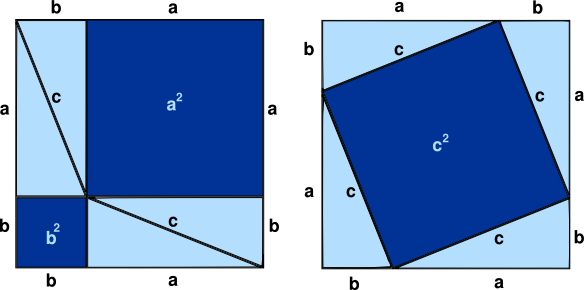
Relación entre los lados de un triangulo rectángulo

¿Qué relación hay entre a, b y c?

El teorema de Pitágoras:

$a^2+b^2=c^2$

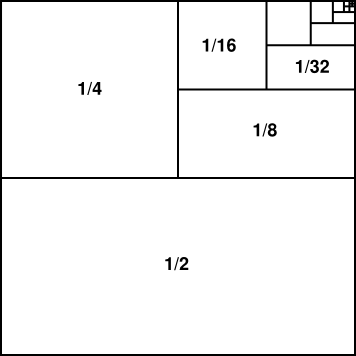
Una serie geométrica

$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+... =1$

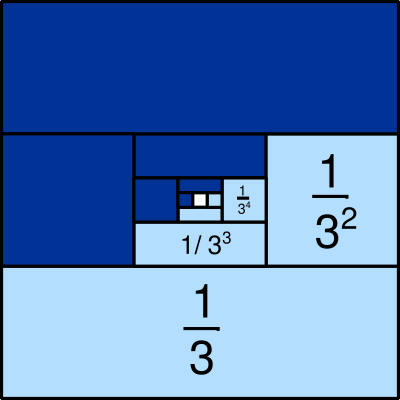
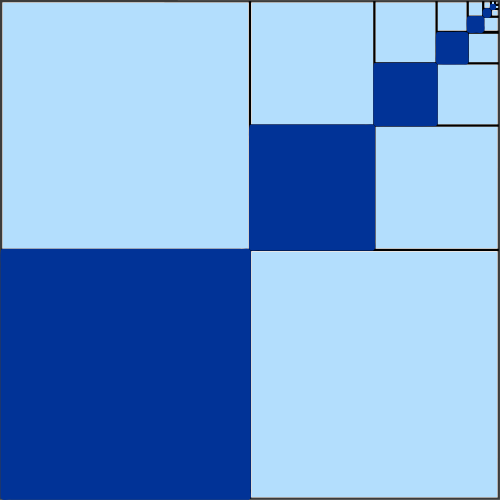
Otra serie geométrica

$\frac{3}{4}+\frac{3}{4}\frac{1}{4}+\frac{3}{4}\left(\frac{1}{4}\right)^{2}+ ... = 1$

Que también podemos expresar:

$1+\frac{1}{4}+\left(\frac{1}{4}\right)^{2}+...=\frac{4}{3}$

Y otra más

$\frac{1}{3} + \frac{1}{{3}^{2}} +\frac{1}{{3}^{3}}+\frac{1}{{3}^{4}}+ \dots = \frac{1}{2}$

y todavía otra

$\frac{1}{4} + \frac{1}{{4}^{2}} +\frac{1}{{4}^{3}}+\frac{1}{{4}^{4}}+ \dots = \frac{1}{3}$

El cuadrado de un binomio

${\left(a+b\right)}^{2}= a^2 + b^2 + 2ab$

Suma de los n primeros impares

$1+3+5+...+ (2n-1)=n*n$

Suma de los n primeros naturales

$1+2+3+...+n= \frac{n( n+1)}{2}$

2 opiniones en “Demostraciones sin palabras: soluciones”

El apartado «SUMA DE LOS N PRIMEROS IMPARES» tiene errores. La expresión debería ser, 1 + 3 + 5 + … + (2n-1) = n*n

Responder

Antonio dice:

27 abril, 2020 a las 1:06 pm

Gracias. Corregido.

Responder

Anónimo dice:

27 abril, 2020 a las 12:15 pm

El apartado «SUMA DE LOS N PRIMEROS IMPARES» tiene errores. La expresión debería ser, 1 + 3 + 5 + … + (2n-1) = n*n

Responder
1. Antonio dice:
  
  27 abril, 2020 a las 1:06 pm
  
  Gracias. Corregido.
  
  Responder