Soluciones a los problemas planteados en la entrada: Ajedrez y matemática recreativa
El problema de las ocho damas
- Colocar sobre un tablero de ajedrez 8 damas de tal forma que no se amenacen entre si, o lo que es lo mismo que en cada fila, columna o diagonal haya como mucho una dama.
- ¿De cuántas maneras distintas se puede resolver el problema anterior?
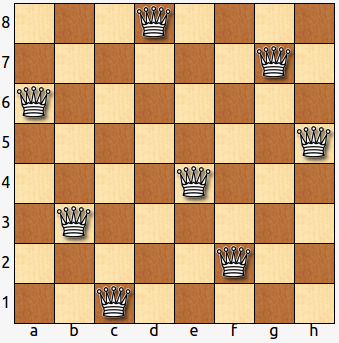
Hay 92 soluciones aunque en esencia son solo 12 ya que las restantes se pueden obtener por reflexiones o rotaciones de una de las 12.
En la Wikipedia se pueden ver las 12 soluciones.
El problema del caballo
- Recorrer con un caballo todo el tablero de ajedrez pasando una sola vez por cada casilla.
- ¿De cuántas maneras distintas se puede hacer el recorrido anterior?
Hay muchas soluciones diferentes. De hecho no se sabe cuantas. Una de ellas se muestra en la figura siguiente:
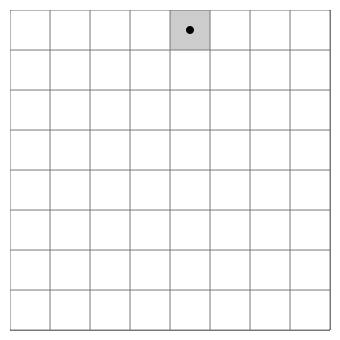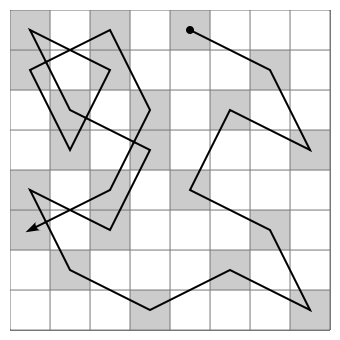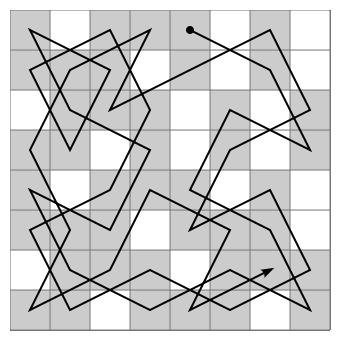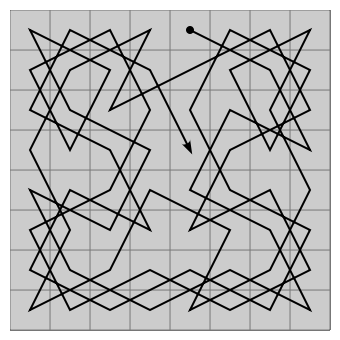
Más información en la Wikipedia
Henry Dudeney
- Todas las casillas del tablero de la figura están ocupadas o atacadas. El problema consiste en sustituir la torre por un alfil en la misma casilla, y luego situar las cuatro damas en otras casillas de tal manera que todas las casillas se encuentren de nuevo ocupadas o atacadas.
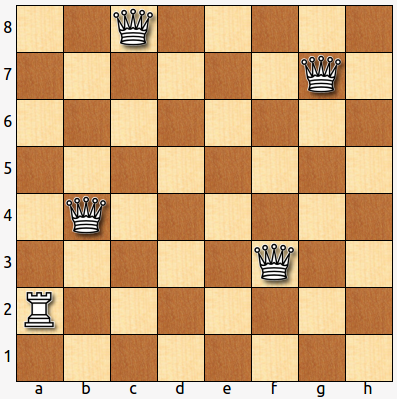
La solución:
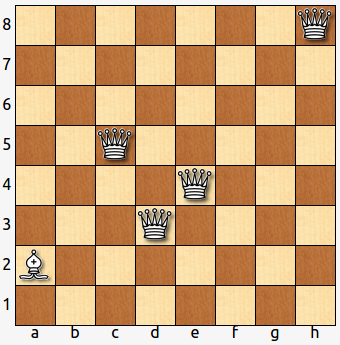
- Coloca ocho alfiles (cuatro negros y cuatro blancos) en un tablero de ajedrez reducido, tal como se ve en la figura. El problema consiste en hacer que los alfiles negros intercambien sus posiciones con los blancos, ningún alfil debe atacar en ningún momento otro del color opuesto. Se deben alternar los movimientos, primero uno blanco, luego uno negro, luego uno blanco y así sucesivamente.
- ¿Cuál es el mínimo número de movimientos en que se puede conseguir?.
Solución: si numeramos las casillas de la siguiente manera:
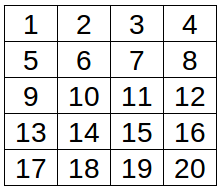la solución viene dada por los movimientos siguientes. Se indica el movimiento de cada pieza entre paréntesis: (casilla de partida-casilla de llegada).
- (18-15)(3-6)
- (17-8)(4-13)
- (19-14)(2-7)
- (15-5)(6-16)
- (8-3)(13-18)
- (14-9)(7-12)
- (5-10)(16-11)
- (9-19)(12-2)
- (10-4)(11-7)
- (20-10)(1-11)
- (3-9)(18-12)
- (10-13)(11-8)
- (19-16)(2-5)
- (16-1)(5-20)
- (9-6)(12-15)
- (13-7)(8-14)
- (6-3)(15-18)
- (7-2)(14-19)
Sam Loyd
En su genial Cyclopedia podemos encontrar entre otros los dos siguientes:
- Un muchacho recibió, como regalo, un tablero de ajedrez que había sido dividido en cuatro piezas de la misma forma y tamaño. Estaban numeradas respectivamente 1, 2, 3 y 4. El muchacho juntó las cuatro piezas formando el tablero que se ve en la figura. El problema consiste en revertir su trabajo, dividiendo el tablero en las cuatro piezas originales, iguales en forma y tamaño, de tal manera que cada una contenga uno de los números. [Pag 298]
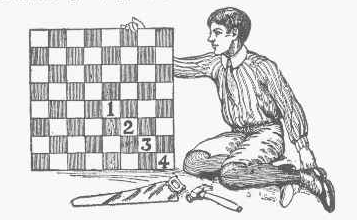
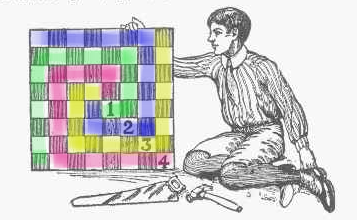
Solución:
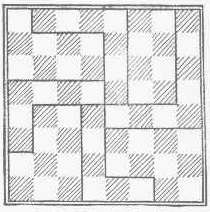
- Loyd nos cuenta una anécdota de la historia francesa en la que el Delfín se salvo de un inminente mate cuando jugaba con el duque de Borgoña rompiéndole el tablero en la cabeza. En el dibujo se ven las ocho partes en que quedó dividido. El problema consiste en recomponer el tablero a partir de los 8 fragmentos. [pag. 97]
Solución:
Ajedrez retrospectivo
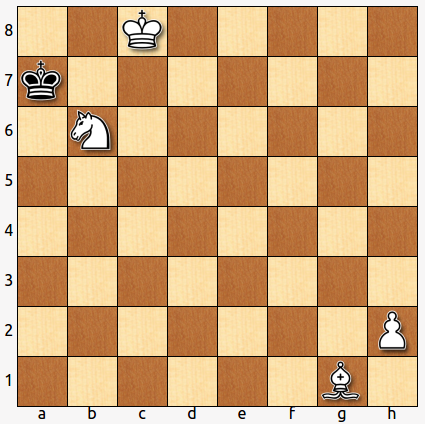
- Si el negro ha sido el último en mover, ¿cuál ha sido su movimiento? ¿y el último del blanco?
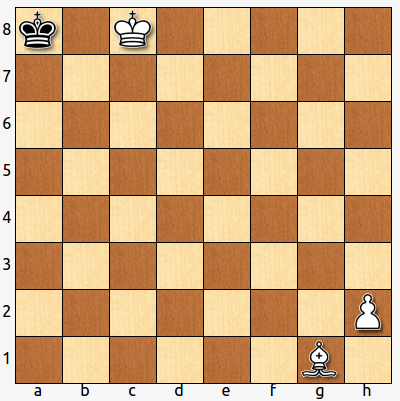
Solución:
Una jugada antes, el tablero tenía la siguiente disposición:
y la continuación:
1. Ca7 RxC
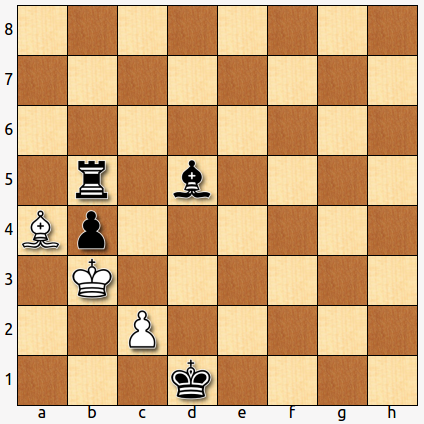
- El rey blanco se ha hecho invisible, ¿dónde está?
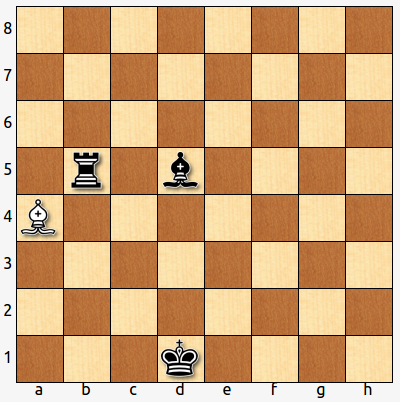
Veamos como se llega a la posición final a partir de la siguiente:
El juego se desarrolla así:
1. … Ad5+ 2. c4 bxc3 2. Rxc3
El rey blanco está pues en c3.
Mucha información sobre retroanálisis en: The Retrograde Analysis Corner
Otros Tipos
- ¿Cuántos cuadrados distintos se pueden construir utilizando como vértices las intersecciones de las líneas del tablero? ¿y rectángulos?
Solución:
- 1 de 8×8
- 4 de 7×7
- 9 de 6×6
- 16 de 5×5
- 25 de 4×4
- 36 de 3×3
- 49 de 2×2
- 64 de 1×1
En total 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 = 204
- ¿Cuántos posiciones distintas pueden formarse con las 32 piezas sobre el tablero? Empezando con 2, luego 3 y así sucesivamente. (Para simplificar no tengamos en cuenta que muchas de ellas no se pueden dar si nos atenemos a las reglas del juego)El número de posiciones es:
4 634 726 695 587 809 641 192 045 982 323 285 670 400 000
Por supuesto, muchas de ellas no se pueden dar en el transcurso de una partida. Por ejemplo aquellas en las que hay peones en blancos en la fila1, peones negros en la fila 8 o no hay dos reyes. Tampoco se tienen en cuenta aquellas en las que se han coronado peones.
Un comentario en “Ajedrez y matemática recreativa: Soluciones”