Hay ciertas ideas matemáticas como por ejemplo, la paridad que aunque simples son muy poderosas y aparecen en la solución de problemas complicados.
A continuación se expone un sencillo, aunque sorprendente, truco matemágico basado en la idea de paridad.
Efecto
El mago pide a un espectador que saque una moneda, el le da otra y le pide que:
- Sin que él lo vea guarde una en cada mano.
- Levante una mano, piense un número, se lo diga y a continuación lo multiplique por el valor de la moneda de la mano que ha levantado.
- Multiplique el valor de la moneda de la otra mano por un número que el mago le dice.
- Le diga el resultado de sumar los dos productos anteriores.
Inmediatamente el mago dice en que mano tiene cada una de las dos monedas.
Explicación
Los números enteros son o pares, divisibles por 2, o impares, no divisibles por 2. Si están representados en el sistema decimal, un número es impar si su última cifra es 1,3,5,7 o 9, y par en caso contrario.
Los números pares e impares cumplen las siguientes reglas:
Suma
par + par = par
par + impar = impar
impar + impar = par
Producto
par x par = par
par x impar = par
impar x impar = impar
- El mago le da al espectador una moneda de distinta paridad que la que ha sacado él. (Así, por ejemplo, si el espectador saca una de 2 céntimos el mago le da por ejemplo una de 5 céntimos)
- El mago le dice al espectador un número de distinta paridad que la del que ha dicho él. (Así, por ejemplo, si el espectador dice 87542 el número del mago podría ser 277)
Llamemos:
mi = valor de la moneda de la mano izquierda.
md = valor de la moneda de la mano derecha.
ni = número por el que se múltiplica el valor de la moneda de la mano izquierda.
nd = número por el que se múltiplica el valor de la moneda de la mano derecha.
pi = vmi x nmi (producto mano izquierda)
pd = vmd x nmd (producto mano derecha)
sf = suma final.
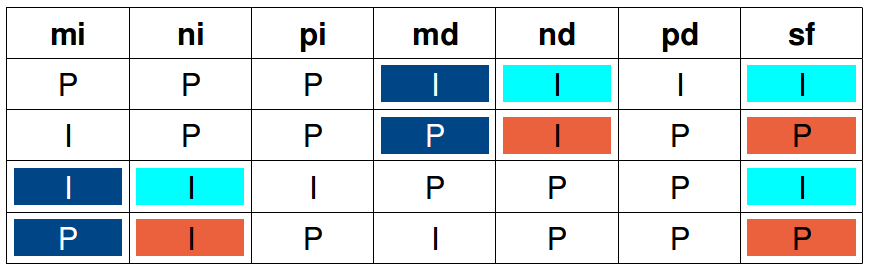
En la tabla se muestran los 4 casos posibles. P e I representan las paridades de los números
O sea que a partir de las paridades de sf, ni e nd podemos deducir en que mano esta cada moneda:
Si sf es impar, buscamos el producto impar (nd o ni) y a su lado está la mano que contiene la moneda de valor impar.
Si sf es par, buscamos el producto impar (nd o ni) y a su lado está la mano que contiene la moneda de valor par.
Si mi y/o md son elevados y al espectador se le deja una calculadora, el efecto será mayor ya que el mago, que solo se fija en la paridad de sf, sabe instantáneamente donde está cada moneda.
Dos problemas
A continuación un par de problemas que se pueden resolver rápidamente con la idea de paridad:
Problema 1
Encontrar 5 números impares cuya suma sea 20.
Problema 2

¿Puede un caballo de ajedrez que está en la casilla inferior izquierda del tablero ir a la casilla superior derecha pasando una sola vez por cada una de las casillas restantes?
Ver pistas