espiral – divulgadores.com

El número e probablemente sea el número más importante en las matemáticas. Aproximado a 5 decimales su valor es 2.71828. No solo es irracional (no se puede expresar como una fracción) sino que, al igual que π, es trascendente (no puede ser raíz de una ecuación polinómica con coeficientes enteros). Es conocido también como número número de Euler ya que Leonhard Euler(1797-1783) fue el primero en estudiarlo y representarlo por la letra e. Aparece en muchos y diferentes lugares pero quizás el más famoso de todos ellos sea la formula de Euler, que relaciona las constantes e y π con los números 0 y 1 así como con la unidad imaginaria i,

$e^{i\pi} +1=0 \$

Como se verá más abajo, una de sus apariciones estelares tiene lugar en la función exponencial,

$y = \textbf{e}^{x} \$

que posee, en exclusiva, la propiedad de que su velocidad de cambio (dy/dx) en cualquier punto tiene el mismo valor que la propia función en ese punto (e^x).

Antes de definirlo veamos algunos lugares sorprendentes en los que emerge.

El problema del secretario

Un empresario va a realizar n entrevistas para contratar a un secretario. Los candidatos serán entrevistados en un orden aleatorio. Al terminar cada entrevista, el empresario debe decidir si contrata a la persona entrevistada o no. Tiene un criterio de selección que permite ordenar, sin empates, a todos candidatos ya entrevistados. Una vez que pase el siguiente candidato ya no podrá contratar a ninguno de los anteriores.

¿Cuál es la estrategia que debe seguir para maximizar las probabilidades de contratar al mejor candidato?

La estrategia optima es la siguiente: descartar los primeros ∼n/e candidatos entrevistados y a continuación seleccionar el primer candidato que sea mejor que los primeros ya entrevistados. Por ejemplo si los candidatos son 100, descartaríamos los 37 primeros,

100/e ≈ 37

y seleccionaríamos al primero de los 63 restantes que fuese mejor que el mejor de los 37 primeros.

Procediendo de esta manera la probabilidad de seleccionar al mejor es aproximadamente 1/e, lo que implica que si se sigue esta estrategia se seleccionará al mejor candidato en torno al 37 % de las ocasiones.

Una versión denominada The Game of Googol apareció en la columna Mathematical Games de febrero de 1960 que Martin Gardner mantenía en la revista Scientific Américan. El juego del Googol sería algo así: Tenemos un pila de n tarjetas que han sido barajadas. Cada una de ellas, en la cara que no vemos, tiene escrito un número diferente. No tenemos ninguna información sobre el rango en el que se mueven los números de las tarjetas que pueden ir desde 1 googol hasta un pequeña fracción de la unidad. Nuestro objetivo es seleccionar la tarjeta que tiene el número mayor. Las reglas son las siguientes: hay que coger una tarjeta, darle la vuelta y observar el número que tiene escrito. En ese momento hay que decidir si se selecciona y el proceso termina, o si se tira a la papelera y se pasa a la siguiente.

¿Cómo podemos maximizar la probabilidad de escoger la tarjeta que tiene el número mayor?

La estrategia es similar a la del problema anterior: descartar, una vez vistas, las ∼n/e primeras tarjetas y a continuación seleccionar la primera tarjeta que tenga un número mayor que los ya vistos. Procediendo de esta manera la probabilidad de seleccionar el número mayor es aproximadamente 1/e, lo que implica que si se sigue esta estrategia se seleccionará el número mayor en torno al 37% de las ocasiones.

Otra aparición sorprendente

Si seleccionamos números al azar en el intervalo [0,1], ¿cuantos necesitaremos, en promedio, para que su suma supera la unidad? La respuesta es e. En el siguiente script en Python se puede ver una simulación,

Y una más

Se genera una secuencia de números al azar en el intervalo [0,1] hasta encontrar uno que sea inferior al anterior. Se cuentan los números de la secuencia incluyendo el último. Por término medio se habrán generado e números.

Primer contacto con el número e

En los libros de enseñanza media se suele introducir como la base de los logaritmos naturales y relacionándolo con una forma de remuneración de una cuenta bancaria:

Supongamos que un banco ofrece un interés del 100 % al dinero que se deposite en sus cuentas y además permite ingresar o retirar dinero en cualquier momento a través de su oficina virtual electrónica .

Si disponemos de 1 € y 1 año de tiempo, ¿qué cantidad como máximo podremos conseguir al final?

Una manera de proceder sería ingresar el euro y esperar un año, el banco nos devolvería nuestro euro y añadiría otro de intereses, en total 2 €.

¿Se puede mejorar? Sí, si al cabo de 6 meses de haber hecho el ingreso cobramos los 0,5 € de intereses y los añadimos el euro inicial, al cabo del año estos 0,5 € que han estado medio año producirán 0,25 €, con lo que en total tendremos 2,25 €.

Si continuamos con esta idea y recogemos los intereses con una frecuencia mayor, reinvirtiendo lo recibido, cada vez recibiremos una cantidad un poco mayor. En la tabla que sigue se puede ver como va aumentando lo que recibimos a medida que aumenta la frecuencia de cobro/reinversión.

nº de veces/año	cantidad final
1	2,0000000
2	2,2500000
3	2,3703704
4	2,4414063
6	2,5216264
12	2,6130353
100	2,7048138
1000	2,7169239
10000	2,7181459
100000	2,7182682
1000000	2,7182805
10000000	2,7182817
100000000	2,7182818

La última cantidad de dinero recibido que aparece en la tabla 2,7182818 es el número e redondeado a 8 cifras.

La forma de calcular la cantidad final que recibiremos del banco si repetimos n veces, a intervalos regulares, el proceso de reinvertir los intereses producidos es

$\left( 1+\frac{1}{n} \right)^n \$

El número e es límite de la expresión anterior cuando n tiende a infinito

$\textbf{e}= \lim\limits_{n\to\infty} \left( 1+\frac{1}{n}\right)^n \$

Si reinvertimos los intereses recibidos de forma continua, lo que se denomina interés compuesto, recibiremos al cabo del año e euros.

Una aproximación con 40 decimales,

e = 2.7182818284590452353602874713526624977572…

Otras formas de definir e

El número e se puede definir a partir de los logaritmos naturales.

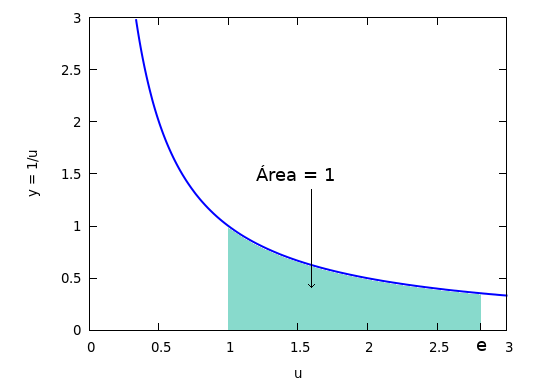
Primero se define la función logaritmo natural como el área bajo la hipérbola y =1/u desde u = 1 hasta u = x, o lo que es lo mismo,

$\ln(x) = \int\limits_1^x \frac{1}{u} \mathrm{d} u \$

y e se define como el número cuyo logaritmo natural es igual a 1,

$\ln(e) = 1 \$

a partir de la definición dada de logaritmo natural,

$1 = \int\limits_1^e \frac{1}{u} \mathrm{d} u \$

e es el número cuyo logaritmo natural es 1 ln(e) = 1

Otra manera de definir e es la siguiente:

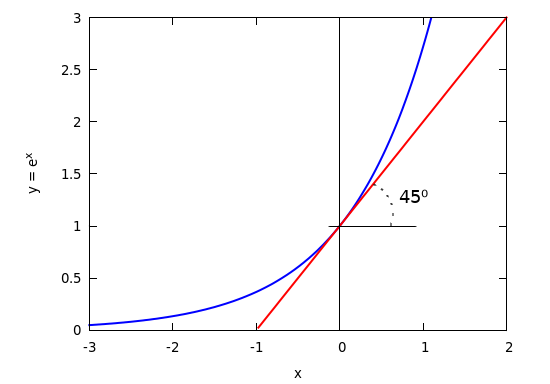
Si la tangente a curva $y = b^x \$ , cuando corta al eje y, tiene una inclinación de 45º, la base b es el número e. O lo que es lo mismo la derivada de $y = b^x \$ en x = 0 tiene el valor 1.

definición del número e — La tangente en x = 0 tiene una inclinación de 45º

Calculando e

De entre las series y fracciones continuas que permiten calcular e, la que Isaac Newton(1642-1727) publicó 1669 es una de las más sencillas,

$\mathrm{e} = \sum\limits_{n=0}^{\infty}\frac{1}{n!}= \frac{1}{0!} + \frac{1}{1!}+ \frac{1}{2!}+ \frac{1}{3!}+ \frac{1}{4!}+\dots \$

La Ciencia y e

e aparece frecuentemente en todas los campos científicos especialmente en situaciones en las que la velocidad de cambio de una cierta magnitud depende del valor de dicha magnitud. A continuación algunos ejemplos,

MODELO LOTKA-VOLTERRA

Alfred J. Lotka(1880-1949) y Vito Volterra (1860-1940) de forma independiente propusieron un modelo matemático para estudiar la dinámica de sistemas en los que existe una competencia entre varias especies. Aplicado con frecuencia sistemas biológicos en los que coexisten dos especies, un depredador y una presa también tiene aplicación a otros campos como la química de reacciones oscilantes en los que en lugar de variaciones en las poblaciones de organismos vivos, se estudian las variaciones en la concentración de especies químicas que de alguna manera también compiten.

En una de sus formas básicas el sistema depredador-presa se representa mediante el siguiente par de ecuaciones diferenciales,

$\frac{d{x}}{d{t}} = \alpha{x}-\beta{xy} \$

$\frac{d{y}}{d{t}} = -\gamma{y}+\delta{xy} \$

x representa número de presas, y, número de depredadores, y t, tiempo.

Las ecuaciones describen las variaciones temporales en las poblaciones de presas y depredadores.

α, β, γ, δ son parámetros que describen el comportamientos de las especies. Representando α, capacidad de reproducción de las presas, β, capacidad de depredación de los depredadores, γ, mortalidad de depredadores y δ, capacidad de reproducción de los depredadores. Analicemos primero lo que sucedería, según el modelo, en dos situaciones particulares, la ausencia de depredadores y la ausencia de presas.

Situación 1: No hay depredadores

Si no hay depredadores la población de presas vendría descrita por,

$\frac{d{x}}{d{t}} = \alpha{x} \$

cuya solución viene dada por la ecuación

$x = x_{0} \textbf{e}^{\alpha t} \$

en la que x0 es la población de presas a t = 0

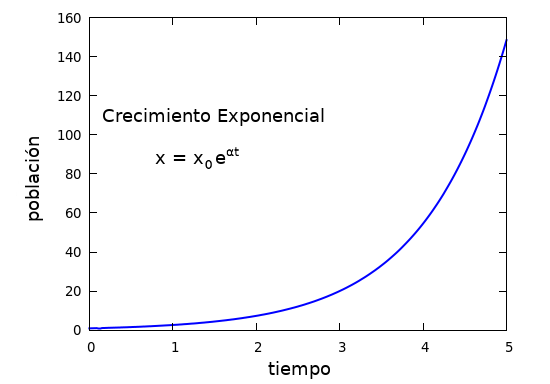
La población de presas, x, crece exponencialmente. Esta forma de crecimiento en una población se denomina crecimiento Malthusiano en honor a Thomas Malthus(1766-1834) y sus teorías demográficas,

Situación 2: No hay presas

Si no hay presas, la población de depredadores se describe mediante,

$\frac{d{y}}{d{t}} = -\gamma{y} \$

con solución,

$y = y_{0} \textbf{e}^{-\gamma t} \$

en la que y₀ representa la población de depredadores a t = 0)

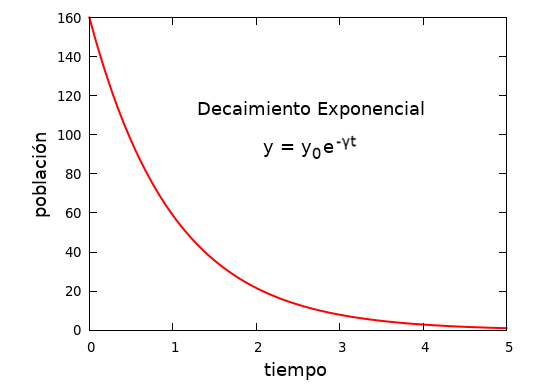
Esta forma de disminución se denomina decaimiento exponencial. La población de depredadores, y, disminuye exponencialmente hasta su desaparición.

Situación 3: Coexisten presa y depredadores

Cuando coexisten presas y depredadores el sistema de ecuaciones diferenciales no se puede resolver analíticamente en términos de funciones elementales. Lo que si es posible es estudiar estos sistemas cualitativa y cuantitativamente y encontrar valores de α, β, γ, δ para los que a partir de valores iniciales de las poblaciones de presas y depredadores se alcanzan situaciones de equilibrio. En la figura puede verse una de estas situaciones de equilibrio en las que las poblaciones de presas y depredadores varían periódicamente.

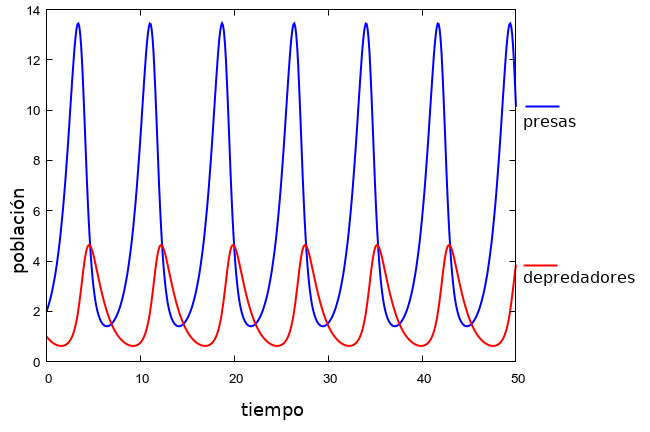
Sistema Lotka-Volterra. Situación de equilibrio en un sistema depredador-presa

En esta situación las poblaciones de presas y depredadores están relacionadas por la siguiente expresión, en la que también e está presente,

$\frac{y^{\alpha}x^{\gamma}}{ \textbf{e}^{\beta y} \textbf{e}^{\delta x}} = \textbf{e}^{K} \$

K representa una constante.

Datación por Carbono-14

Los vegetales toman constantemente carbono de la atmósfera, en forma de dióxido de carbono, y lo incorporan a sus tejidos. A través de la cadena alimenticia, este carbono está presente también en los animales. El carbono atmosférico contiene una pequeña parte de carbono radiactivo: el isótopo Carbono-14 (C-14). El C-14 atmosférico se forma por la acción de los rayos cósmicos sobre el nitrógeno atmosférico. Mientras el vegetal está vivo, la proporción de C-14 es la misma que en la atmósfera. Cuando muere, la cantidad de C-14 disminuye paulatinamente con el tiempo debido a la desintegración radiactiva. De este modo, la proporción de C-14 en un resto de algo que en un tiempo pasado fue un ser vivo permite conocer cuanto hace que ha muerto.

¿Qué relación hay entre la cantidad de C-14 presente en una muestra en un instante t₀ y la cantidad presente cuando ha pasado un tiempo t?

Una muestra radiactiva se desintegra en un proceso de decaimiento exponencial que como se ha visto más arriba quiere decir que la velocidad a la que se desintegran los átomos de la substancia en un momento dado depende de la cantidad de átomos presentes en ese instante. Esto es lo que refleja la siguiente ecuación diferencial,

$\frac{d{N}}{d{t}} = -\lambda N \$

N es el número de átomos C-14 presentes en un momento dado y λ es la constante de desintegración radiactiva que mide la probabilidad de que un átomo se desintegre. λ es la inversa del tiempo de vida media,τ ,que representa el tiempo medio que tarda un átomo radiactivo en desintegrarse.

La solución de la ecuación diferencial anterior es,

$N = N_{0} \textbf{e}^{-\lambda t} \$

en la que N₀ representa el número de átomos cuando t = 0.

Si la expresamos en función del tiempo de vida media,

$N = N_{0} \textbf{e}^{-\frac{t}{\tau}} \$

despejando t y teniendo en cuenta que el tiempo de vida media para el C-14 es τ = 8267 años,

$t =8267\ln(\frac{N_0}{N}) \$

Conociendo el número de átomos de C-14 que había en la muestra cuando el organismo estaba vivo(N₀) y el número de átomos que hay en la actualidad (N), se puede saber el tiempo (t) que ha transcurrido.

Absorción del sonido al atravesar un medio

Cuando el sonido atraviesa un medio su intensidad disminuye ya que una parte de la energía de la onda sonora se disipa en forma de calor. La variación de la intensidad sonora, I, con la distancia, x, al atravesar el medio es proporcional a la propia intensidad ,

$\frac{d{I}}{d{x}} = -\beta I \$

La solución a la ecuación diferencial anterior viene dada por,

$I = I_{0} \textbf{e}^{-\beta x} \$

siendo I₀ la intensidad sonora al entrar en el medio y β el coeficiente de absorción que es propio de cada medio.

Algo parecido sucede también con las ondas electromagnéticas como establece la ley de Beer–Lambert.

Alguna curva famosa con e en su ecuación

La Catenaria

Si se cuelga una cuerda, cable o cadena entre dos puntos, adopta la forma de una curva denominada catenaria.

La ecuación de una catenaria en coordenadas cartesianas es,

$y = \frac{a(\textbf{e}^{\frac{x}{a}} +\textbf{e}^{-\frac{x}{a}} )}{2} \$

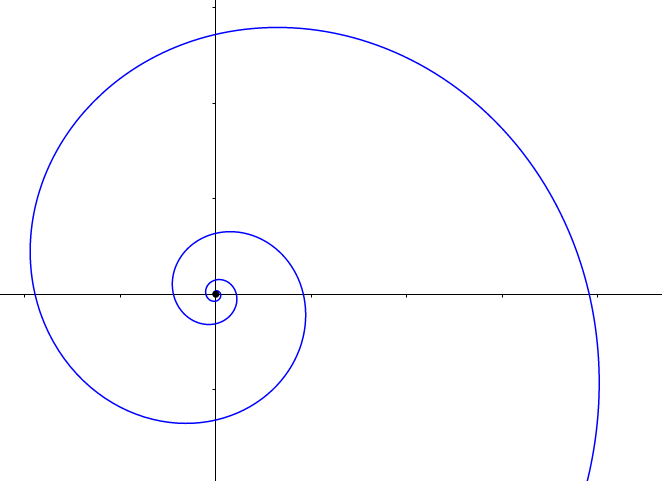
La espiral logarítmica

La espiral logarítmica es una curva que podemos ver frecuentemente en la naturaleza. Aparece en la forma de nuestra galaxia, la Vía Láctea, y otras galaxias espirales. Está también presente en la concha de muchos moluscos y vegetales como el romanesco o en el aspecto que presenta un huracán y otras formaciones atmosféricas vistas desde el espacio. Aunque Descartes la mencionó por primera vez, fue estudiada a fondo por Jacob Bernouilli que la llamó Spira mirabilis (Espiral maravillosa).

Este último quiso que apareciese inscrita en su tumba con el texto latino Eadem mutata resurgo (Aunque cambiada resurjo la misma), que hace referencia a que la espiral no cambia de forma aunque cambie de tamaño. El grabador que no debía tenerla a mano inscribió en su lugar una espiral de Arquímedes.

La ecuación de la espiral logarítmica en coordenadas polares es, $r = a \textbf{e}^{b\theta} \$ en la que a y b representan dos constantes positivas.

En el crecimiento del romanesco aparece la espiral logarítmica

Ramanujan y e

Y como colofón una fórmula en la que el número e aparece acompañado de otros populares colegas: 0, 1, 2, π y el número áureo, φ. En una de las cartas que Srinavasa Ramanujan(1887-1920) envió a G.H. Hardy(1877-1947) aparecen tres fórmulas de las que Hardy dice: Nunca había visto nada parecido. Un simple vistazo es suficiente para comprobar que únicamente podrían haber sido escritas por un matemático de la clase más alta. Deben ser ciertas porque, si no lo fueran, nadie tendría la imaginación para inventarlas. Una de ellas es la siguiente,

$\frac{1}{1+\frac{\textbf{e}^{-2\pi}}{{1+\frac{\textbf{e}^{-4\pi}}{1+\dots}}}}-\left(\sqrt{2+\varphi}-\varphi\right)\textbf{e}^{\frac{2}{5}\pi}=0 \$

Para saber más

Anisiu, M.C. 2014. Lotka, Volterra and their model. Didactica Mathematica, Vol. 32(2014), pp. 9–17.
Clawson, C.C. 1996. Mathematical Mysteries. The Beauty and Magic of Numbers. Perseus Books.
Darling, D. 2004. The Universal Book of Mathematics. Wiley.
Ferguson, T. S. (1989). Who solved the secretary problem?. Statistical Science. 4 (3): 282–296.
Gardner, M. 1966. The game of Googol en New Mathematical Diversions. Simon and Schuster. Hay traducción al español
- Gardner, M. 1981. Nuevos pasatiempos matemáticos. Alianza Editorial: El libro de bolsillo 391.
Gardner, M. 1969. The transcendental number e en The Unexpected Hanging and Other Mathematical Diversions. Simon and Schuster. Hay traducción al español
- Gardner, M. 1991. El trascendental número e en El ahorcamiento inesperado y otros entretenimientos matemáticos. Alianza Editorial: El libro de bolsillo 1549.
Hardy, G.H. 1959.Ramanujan; twelve lectures on subjects suggested by his life and work. Chelsea Publishing Company.
Maor, E. 1994. e: The story of a number. Princeton University Press.
Shultz H.S. and B. Leonard. 1989. Unexpected Occurrences of the Number e. Mathematics Magazine, October 1989, Volume 62, Number 4, pp. 269–271.

Etiqueta: espiral

El número e