
En 1897 la Cámara de Representantes del estado de Indiana aprobó por unanimidad el proyecto de ley nº 246 de la legislatura en cuyo preámbulo se puede leer:
«Un proyecto de ley que presenta una nueva verdad matemática y la ofrece como una contribución a la educación que solamente podrá usar el estado de Indiana sin tener que pagar ningún tipo de derechos, siempre y cuando se apruebe en la actual legislatura de 1897.»
Los políticos son gente muy ocupada y ante tal ofrecimiento no vieron ninguna razón para no aceptarlo. Si hubiesen seguido leyendo quizás se hubiesen sorprendido un poco. En la sección 3 se afirmaba:
«Una prueba más del valor de la contribución propuesta por el autor a la educación, y ofrecida como regalo al Estado de Indiana, es el hecho de que sus soluciones de la trisección del ángulo, la duplicación del cubo y cuadratura (del círculo) han sido aceptadas como contribuciones a la ciencia por la American Mathematical Monthly, el máximo exponente del pensamiento matemático en este país. Y recuérdese además que las instituciones científicas hace tiempo que se han rendido ante estos problemas por ser misterios insondables que están por encima de la capacidad compresora del hombre«
A lo largo del proyecto de ley en un lenguaje farragoso se pretendía cuadrar el círculo implicando con ello un nuevo valor para Pi, aunque no estaba muy claro cual era el valor correcto que su autor quería establecer ya que de su lectura se pueden deducir varios. David Singmaster, que analizó este proyecto y el trabajo que el autor del mismo envió a la revista American Mathematical Monthly encontró hasta 9 valores distintos de Pi entre ambos.
El proyecto de ley una vez aprobado siguió su camino hacia el senado donde se hubiese convertido en ley si no fuese por que, de casualidad, llegó a manos del profesor C.A. Waldo, director del departamento de matemáticas de la Universidad de Purdue, que estaba de visita en el senado gestionando la aprobación del presupuesto de su universidad. Waldo quedó asombrado por el contenido del proyecto y transmitió a los senadores su opinión sobre el mismo. Consecuentemente, el debate final del proyecto quedo pospuesto sine die.
El autor y promotor del proyecto de ley fue el médico Edwars Johnston Godwin. En 1894 apareció su trabajo, Cuadratura del círculo, en la revista American Mathematical Monthly, volumen 1 (pag. 246-247), no en la sección de artículos sino en la sección Queries and Information en la que se publicaba un batiburrillo de material que recibían los editores.
La cuadratura del círculo
El problema de la cuadratura del círculo es un problema muy antiguo:
Dado un determinado círculo construir con regla y compás un cuadrado que tenga la misma área.
En 1882 Ferdinand von Lindemann probó que Pi era un número trascendente, lo que significa literalmente que no puede ser una raíz de un polinomio con coeficientes racionales. Una de las consecuencias de que Pi sea un número trascendente es que cuadrar el círculo es imposible.
Otras construcciones imposibles
Las otras construcciones clásicas con regla y compás también imposibles que se mencionan en el proyecto son:
La duplicación del cubo
Determinar con regla y compás el lado de un cubo tal que su volumen sea el doble del volumen de otro cubo de lado dado.
La trisección del ángulo
Dividir, con regla y compás, un ángulo dado en tres más pequeños del mismo tamaño.
Un ejemplo de construcción posible con regla y compás
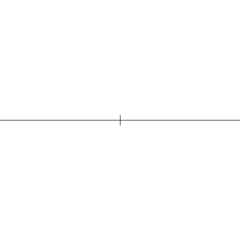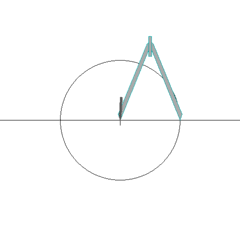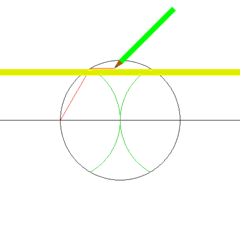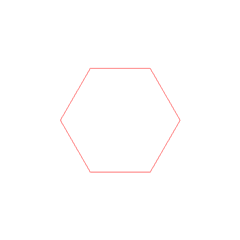
Un problema soluble con regla y compás que podemos ver en la figura adjunta es el siguiente:
Dado su lado construir, con regla y compás un hexágono regular.
Más información
- Underwood Dudley. Mathematical Cranks. 1992.(Washingthon: The Mathematical Association of America)
- David Singmaster. The Legal Values of Pi. The Mathematical Intelligencer, 7, no. 2 (1985), 69–72.
- The Indiana Pi Bill 1897. Página en la web del gobierno de Indiana.
Creditos
El autor de la imagen Construcción con regla y compás es Aldoaldoz y está distribuida con una licencia CC BY-SA 3.0.
