¿Cómo se hace el truco?
El mago saca una baraja de su caja y se la pasa a varios espectadores para que la corten. Después del último corte reparte las 5 cartas superiores entre el público.
El mago saca entonces un teléfono y dice disponer de una aplicación experimental que tiene capacidades telepáticas. La aplicación está todavía en fase de desarrollo, dice el mago, y todavía no puede distinguir bien los colores de las cartas. Debido a esta circunstancia pide a cada uno de los espectadores que han recibido una carta que diga si es negra o roja. Mientras lo van haciendo el mago dirige su móvil hacía ellos dando la sensación de que los está escaneando.
Cuando los 5 espectadores han acabado de decir el color de su carta, el mago muestra la pantalla de su teléfono. En ella aparecen las 5 cartas que tienen los espectadores.
Explicación
Preparación
De una baraja francesa se seleccionan las 32 cartas siguientes y se disponen en el orden en que se muestran,
| 8♣ | A♣ | 2♣ | 4♣ | A♠ | 2♦ | 5♣ | 3♠ |
| 6♦ | 4♠ | A♥ | 3♦ | 7♣ | 7♠ | 7♥ | 6♥ |
| 4♥ | 8♥ | A♦ | 3♣ | 6♣ | 5♠ | 3♥ | 7♦ |
| 6♠ | 5♥ | 2♥ | 5♦ | 2♠ | 4♦ | 8♠ | 8♦ |
Desarrollo
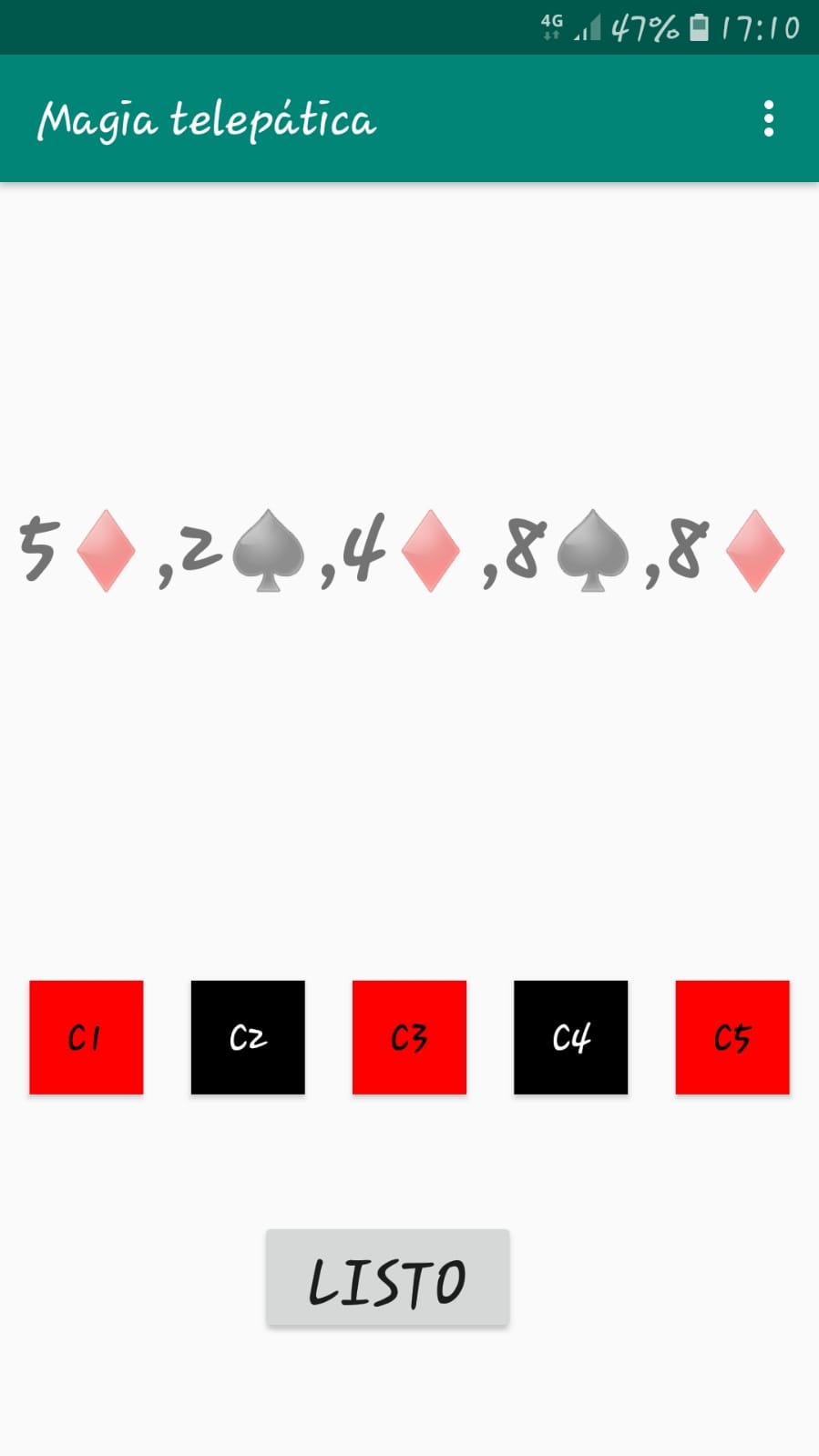
Se procede como se describe más arriba en el apartado ¿Cómo se hace el truco?. Cuando el mago reparte las cartas les asigna mentalmente un número del 1 al 5. Para luego poder recordar fácilmente este número, el reparto se ha de realizar siguiendo un cierto orden, por ejemplo desde la izquierda hacia la derecha de la sala. Cuando cada espectador va diciendo el color de su carta, y el mago aparenta escanear la mente del espectador, lo que hace realmente es pulsa el botón correspondiente al número de la carta si el espectador dice que la suya es roja.

Al acabar con la 5ª carta, el mago pulsa el botón LISTO y es en ese momento, al aparecer solo las 5 cartas, como se ve en la captura de la derecha, cuando enseña la pantalla del móvil al público.
Puedes descargar la aplicación desde el enlace que sigue,

¿Por qué funciona?
Sucesiones de de Bruijn
Una sucesión de de Bruijn de orden n que usa un alfabeto de k símbolos, abreviadamente B(k,n) es una sucesión cíclica en la que todas las subsucesiones posibles de longitud n ocurren una y sola una vez. El nombre hace referencia al matemático holandes Nicolaas Govert de Bruijn (1918-2012).
Hay sucesiones de de Bruijn B(k,n) diferentes.
Por ejemplo, una sucesión de de Bruijn de orden 2 que usa un alfabeto de 2 símbolos, R y N, sería RNNR. Qué la sucesión sea cíclica quiere decir que a la última R le sigue la primera R como se ve en la siguiente figura. Empezando por la N a la izquierda y siguiendo el sentido de las agujas del reloj nos vamos encontrando las cuatro posibles subsucesiones de 2 símbolos que son NR,RR,RN y NN.

Sucesión de de Bruijn B(2,5)
Una sucesión de de Bruijn B(2,5) tiene una longitud de 25 =32. Este número es también el de las subsucesiones diferentes de 5 elementos que contiene. Hay 2048 sucesiones B(2,5) posibles. Usando el mismo alfabeto anterior {R,N} una de ellas es la siguiente,
NNNNNRNNRNRRNNRRRRRNNNRRNRRRNRNR

En la sucesión anterior aparecen una sola vez todas las subsucesiones posibles de 5 elementos como por ejemplo, NNRRR o RNNNR.
Si se toman 32 cartas de una baraja francesa, 16 rojas y 16 negras, y se ordenan de tal forma que los colores de sus cartas reproduzcan la sucesión anterior, como la sucesión es cíclica, es posible cortar todas las veces que se quiera sin que la sucesión se altere.
Con una baraja así preparada, si somos capaces de memorizarla, se pueden identificar 5 cartas consecutivas cualesquiera solo con conocer el orden de sus colores, ya que como se ha visto es único.
Persi Diaconis y Ron Graham en su libro Magical Mathematics presentan la sucesión B(2,5) anterior usando las 32 cartas y el orden que se muestra en la tabla que se puede ver más arriba.
Con esta disposición de cartas concreta (no solo de colores), Diaconis y Graham explican cómo es posible, sin tener que memorizar toda la sucesión, deducir las cinco cartas.
Con esta aplicación el truco se simplifica ya que el mago no necesita memorizar nada. Se utiliza la misma disposición de cartas que utilizan Diaconis y Graham en su libro por si alguien se anima utilizar su método. En la app, dado que es ella la que memoriza la disposición de las cartas, se podría haber utilizado cualquier otras con la única condición de que siguiese la sucesión de colores indicada por una de las 2048 sucesiones B(2,5)
Para saber más
- Diaconis P., R. Graham.2012. Magical Mathematics. Princeton University Presss.
- DivulgaMat: Sucesiones De Bruijn
Google Play y el logotipo de Google Play son marcas comerciales de Google LLC.
