La dinámica de fluidos estudia el movimiento de los fluidos así como él de los objetos en su interior. Aire y agua son fluidos y prácticamente todo lo que nos rodea o es un fluido o se mueve en él. Objeto de estudio de la dinámica de fluidos son cosas tan diversas como el vuelo de un avión, la circulación de la sangre, las tuberías de un edificio, un ventilador o el vuelo de una bola de golf .
Aunque los principios físicos que se utilizan en la dinámica de fluidos son los ya conocidos como la conservación de la masa, la conservación de la energía o las leyes de la mecánica de Newton, su aplicación al movimiento de los fluidos da lugar en ocasiones a problemas para los que todavía no se conoce solución. El más famoso de ellos es un antiguo problema, que data del S XIX, la solución de las Ecuaciones de Navier-Stokes.
Para poder contestar a la pregunta que da título a esta entrada y a otras relacionadas se revisan algunos conceptos como el de línea y tubo de flujo, los tipos de flujo o el número de Reynolds. Se verá como al realizar ciertas simplificaciones, los ya conocidos principio de conservación de la masa y principio de conservación de la energía al aplicarlos a los fluidos dan lugar a la Ecuación de Continuidad y a la Ecuación de Bernoulli. Con ellas y algunas ideas como la de capa límite es posible analizar las diversas situaciones que surgen en las preguntas que se plantean.
A continuación algunas preguntas a las que se da respuesta en la entrada.
Las preguntas
- ¿Por qué en una zona profunda de un rio el agua se mueve mucho más despacio que en una zona de poco profundidad?
- ¿Por qué el chorro de agua que sale de un grifo se va haciendo más estrecho a medida que cae?
- ¿Por qué es peligroso estar cerca de una vía férrea si va a pasar un tren a gran velocidad?
- ¿Por qué un fuerte viento suele levantar un tejado en lugar de hundirlo?
- ¿Por qué una pelota de ping-pong se puede mantener flotando en el chorro de un secador de pelo dirigido hacia arriba?
- ¿Por qué si damos un pequeño empujón lateral a la pelota esta vuelve al centro del chorro de aire?
- ¿Por qué las bolas de golf tienen alvéolos?
- ¿Por qué los balones de futbol tienen costuras?
- ¿Cómo se puede conseguir un tiro curvo en fútbol?
- ¿Cómo es posible que una vez golpeada una bola de golf gire a izquierda o derecha o se desplace en línea recta?
- ¿Cómo se puede lanzar en béisbol una pelota recta o curva?
- ¿Por que hay barcos que en lugar de velas tienen cilindros rotatorios?
¿Qué es un fluido?
Un fluido es una substancia como el agua o el aire que pueden deformarse constantemente y literalmente fluir.
Ecuación de Continuidad
Las lineas de flujo son una herramienta para visualizar el comportamiento de un fluido. Son líneas que se dibujan de forma que la velocidad del fluido en cada punto es tangente a la línea de flujo que pasa por él. Su densidad (nº de líneas/ unidad de superficie, o volumen si la representación es tridimensional) es proporcional a la velocidad del fluido. Tal como están definidas no se pueden cortar ya que eso implicaría que en ese punto el fluido tendría dos velocidades distintas, algo que no tiene sentido.
Las lineas de flujo representan las trayectorias que siguen las partículas del fluido.
En la figura se representa una región de fluido con forma de tubo. Su parte exterior está limitada por lineas de flujo, y como consecuencia de esto, el fluido no la atraviesa y de ahí su nombre, tubo de flujo.

Pese a no ser un tubo real, el tubo de flujo se comporta como si lo fuera.
La ecuación de continuidad es una relación entre las áreas, A1 y A2 de los extremos del tubo y la velocidad del fluido en las mismas, v1 y v2. Es una consecuencia de la conservación de la masa. En un tiempo dado, la masa de fluido que entra por 1 ha de ser la misma que sale por 2.
A1 v1 = A2 v2
¿Cómo se deduce de la conservación de la masa?
En un tiempo Δt la masa de fluido que entra por 1 ha de ser igual que la que sale por 2. Llamando V al volumen y ρ a la densidad,
por 1 entra, m1 = V1ρ1 = A1 v1 Δt ρ1
por 2 sale, m2 = V2ρ2 = A2 v2 Δt ρ2
igualando,
A1 v1 Δt ρ1 = A2 v2 Δt ρ2
si la densidad del fluido no varía (es incompresible), ρ1 = ρ2
A1 v1 = A2 v2
Esta relación permite contestar a las dos primeras preguntas planteadas:
¿Por qué en una zona profunda de un rio el agua se mueve mucho más despacio que en una zona de poco profundidad?
Como en la zona profunda la sección es mayor, la velocidad debe ser menor para que se cumpla la ecuación de continuidad.
¿Por qué el chorro de agua que sale de un grifo se va haciendo más estrecho a medida que cae?
De nuevo la ecuación de continuidad nos da la respuesta. Debido a la fuerza de la gravedad el agua que sale del grifo se mueve cada vez más deprisa. La sección del chorro, de acuerdo a la ecuación de continuidad, ha de ser cada vez menor.

Ecuación de Bernoulli
Daniel Bernoulli (1700-1782) fue un matemático y físico que en 1738 publicó su obra Hydrodynamica dedicada a la dinámica de fluidos. En ella expone el comportamiento de un fluido ideal (incompresible y sin viscosidad) que fluye en regimen láminar. En 1752 el matemático y físico Leonhard Euler(1707-1783) expresó el comportamiento descrito por Bernoulli en la forma que hoy en día nos resulta familiar,
P +½ρv2 + ρgy= constante
Siendo P, la presión , ρ la densidad v, la velocidad e y la altura del fluido. g es la aceleración de la gravedad.
La ecuación de Bernoulli es una forma de expresar el principio de conservación de la energía para los fluidos en movimiento.
En la ecuación aparecen, referidos a la unidad de volumen, los tres tipos de energía que puede tener un fluido ideal: energía potencial de presión, P, energía cinética ½ρv2, y energía potencial gravitatoria, ρgy .
En aplicación del principio de conservación de la energía, su suma ha de permanecer constante.
La ecuación de Bernoulli se escribe con frecuencia referida a dos elementos del fluido en los puntos 1 y 2:
P1 + ½ρv12 + ρgy1 + = P2 + ½ρv22 + ρgy2
Si los puntos del fluido que consideramos están a la misma altura, y1 = y2, la ecuación quedaría reducida a:
P1 + ½ρv12 = P2 + ½ρv22
de donde se deduce un resultado, que puede resultar paradójico:
Si aumenta la velocidad del fluido su presión disminuye y viceversa:
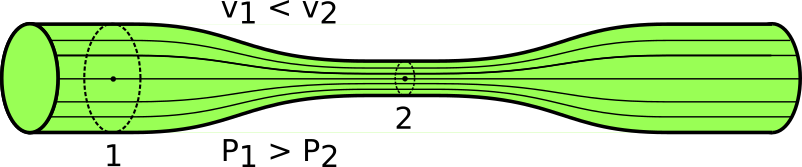
Fig 3. Si aumenta la velocidad del fluido su presión disminuye y viceversa
La ecuación, que aunque estrictamente es solo aplicable a fluidos ideales en régimen laminar, es un buen punto de partida para analizar muchas situaciones que se dan con frecuencia en el movimiento de líquidos y gases.
¿Cómo se deduce la Ec. de Bernoulli de la Conservación de la Energía?
La ecuación de Bernoulli es la aplicación del principio de conservación de la energía al movimiento de un fluido ideal.
Para deducirla se aplica el teorema de la energía cinética a una porción de fluido en el interior de un tubo de flujo:
El trabajo realizado por las fuerzas externas se emplea en variar la energía cinética del fluido.
En el tubo de flujo de la figura, en un intervalo de tiempo Δt, un pequeño volumen de fluido, V, entrará por 1 y, dado que su densidad no varía al ser ideal, la misma cantidad saldrá por 2.
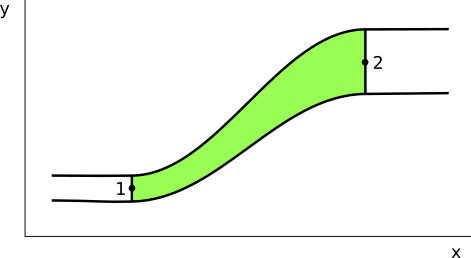
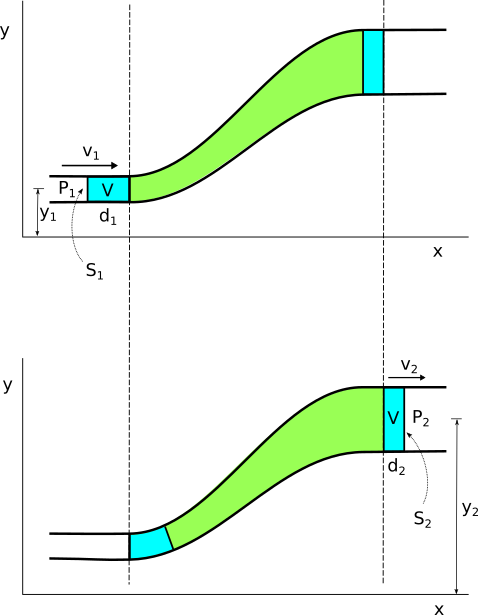
¿Qué fuerzas externas actúan sobre el fluido considerado?
Siendo P la presión del fluido, ρ su densidad, S la sección del tubo, d la distancia recorrida y V el volumen del fluido que entra y sale del tubo, las fuerzas externas son:
1. La fuerza que el resto del fluido ejerce en 1.
2. La fuerza que el resto del fluido ejerce en 2.
3. La fuerza que hace la Tierra, el peso del fluido.
Calculemos los trabajos que las 3 fuerzas hacen sobre el fluido.
En el extremo 1: W1 = P1S1d1 = P1V
En el extremo 2: W2 = −P2S2d2 = − P2V
El trabajo que hace el peso cuando entra un volumen V de fluido en 1 y sale por 2 es:
Wp = − Vρg(y2−y1)
Los dos últimos trabajos son negativos ya que, en ambos casos, fuerza externa y desplazamiento del fluido tienen sentidos opuestos.
Según el teorema de la energía cinética
Wfuerzas externas = ΔEc
P1V − P2V − Vρg(y2−y1) = ½mv22 – ½mv12
dividiendo por el volumen del fluido, V,
P1 − P2 − ρg(y2−y1) = ½ρv22 – ½ρv12
separando términos se llega a la expresión habitual,
P1 + ½ρv12 + ρgy1 + = P2 + ½ρv22 + ρgy2
¿Por qué es peligroso estar cerca de una vía férrea si va a pasar un tren a gran velocidad?
Cuando el tren circula, el aire que está entre nosotros y el tren es arrastrado por este y su velocidad es mayor que la del aire que tenemos detrás de la parte de nuestro cuerpo más alejada del tren. De la ecuación de Bernoulli se deduce que a menor velocidad del aire mayor presión y viceversa. Esa diferencia de presiones nos empujará hacia el tren.
¿Por qué un fuerte viento suele levantar un tejado en lugar de hundirlo?
La razón es la misma dada en la respuesta anterior. La diferencia de velocidades del aire entre la parte exterior del tejado y la interior hace que también exista una diferencia de presiones que es la que levanta el tejado. Una posible solución sería abrir las ventanas del edificio para tratar de conseguir que circulase aire también en la parte interior del tejado disminuyendo así la diferencia de presión.
¿Por qué una pelota de ping-pong se puede mantener flotando en el chorro de un secador de pelo dirigido hacia arriba?
Cuando el chorro de aire procedente del secador choca contra la pelota su velocidad disminuye. Por el principio de Bernoulli su presión aumenta ejerciendo una fuerza sobre la pelota que iguala su peso.
¿Por qué si damos un pequeño empujón lateral a la pelota esta vuelve al centro del chorro de aire?
Al empujar un poco la pelota, la parte de la misma más alejada del centro se encuentra con aire más lento (a mayor presión) que la devuelve al centro.
Los fluidos no siempre fluyen igual
Cuando un fluido fluye es fácil observar que lo puede hacer de dos formas diferentes:
Flujo laminar, literalmente en láminas. Las capas del fluido deslizan unas sobre otras suavemente. Dos zonas contiguas del fluido mantienen la distancia que las separa. Se puede ver en un rio cuando la profundidad es grande.
Flujo turbulento. El flujo cambia constantemente y aparecen remolinos. Las zonas contiguas no mantienen su distancia y se mueven independientemente en direcciones impredecibles. Siguiendo con el ejemplo del río, el agua en la zonas poco profundadas fluye con un flujo turbulento.
La imagen contigua muestra una fotografía Schlieren en la que se ve fluir el aire caliente producido en la combustión de una vela. Inicialmente el flujo es laminar y en el último tercio de la imagen se produce el tránsito a turbulento. (La foto la ha realizado el Dr Gary Settles)

El número de Reynolds
El que el flujo sea laminar o turbulento depende de la relación entre las fuerzas de presión y las fuerzas de rozamiento interno o fuerzas viscosas .
Las fuerzas de presión, proporcionales a la velocidad y densidad del fluido, favorecen el flujo turbulento mientras que las fuerzas de rozamiento interno del fluido, que es lo que mide su viscosidad, favorecen el laminar.
Osborne Reynolds (1842-1912) se dio cuanta de que se podían combinar los factores que influyen en el cambio de régimen en un número sin dimensiones, que hoy lleva su nombre.
El número de Reynolds, Re, permite caracterizar el tipo de flujo y determinar cuando se producirá la transición entre el régimen laminar y el turbulento. Se puede definir de varias maneras en función de la situación que se estudia.
Para un fluido que circula por una tubería de sección circular:
siendo v, la velocidad, ρ, la densidad y μ, la viscosidad dinámica del fluido y D, el diámetro de la tubería.
Para una bola sólida que se mueve en el interior de un fluido
siendo D el diámetro de la bola, v, su velocidad con respecto al fluido, ρ, la densidad del fluido y μ, la viscosidad dinámica de este.
Para esta situación
| Número de Reynolds | Tipo de Flujo |
| Re < 2000 | Laminar |
| 2000 > Re > 4000 | zona de transición |
| Re > 4000 | Turbulento |
Objetos que se mueven en un fluido
Cuando algo se mueve en el seno de un fluido experimenta una fuerza resultado de la interacción con este. Al estudiar esta interacción es equivalente considerar que el fluido se mueve y el objeto está en reposo, que el que se mueve es el objeto y el fluido está en reposo o que ambos se mueven y algo externo es lo que está en reposo. Lo habitual es considerar que el objeto esta en reposo y es el fluido el que se mueve. Esto es lo que se hace por ejemplo en un túnel de viento.
Habitualmente la fuerza que el fluido hace sobre el objeto se suele descomponer en dos, una en la dirección del movimiento y opuesta a la velocidad, arrastre, y otra en dirección perpendicular, sustentación. En la figura adjunta se muestran en el caso de la fuerza del aire sobre un ala. El nombre sustentación puede llevar a engaño en ciertos casos ya que como veremos más abajo, la sustentación no necesariamente es vertical.
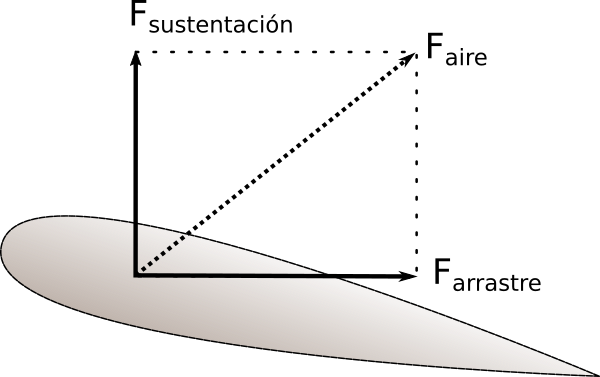
La fuerza de arrastre depende de la velocidad relativa. A velocidades bajas es proporcional a dicha velocidad mientras que a velocidades mayores es proporcional a su cuadrado y se suele expresar de la siguiente manera:
F = ½CDρv2
siendo ρ la densidad del fluido, v su velocidad y CD el coeficiente de resistencia o arrastre (Drag en inglés), una cantidad sin dimensiones que caracteriza la resistencia que ofrece un cierto objeto en un fluido.
La crisis del arrastre
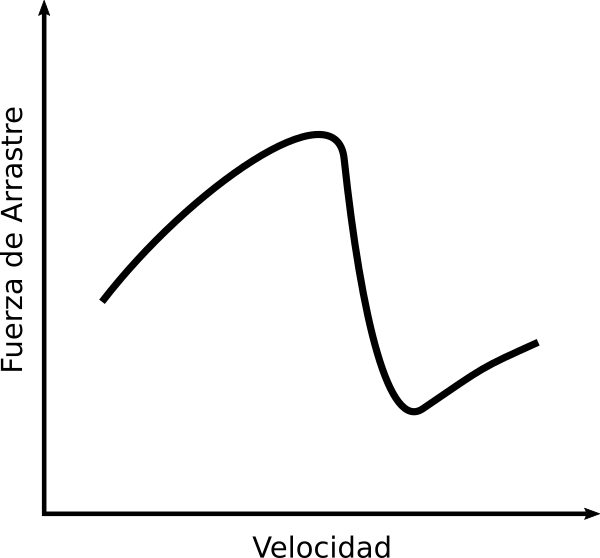
A principios del S XX Gustave Eiffel(1832-1923) montó en la base de su torre un laboratorio en el que en 1909 construyó un túnel de viento. En uno de sus experimentos, al estudiar cómo variaba la fuerza de arrastre que experimentaba una bola a medida que lo hacía la velocidad del aire, observó que al aumentar esta última llegaba un momento en el que la fuerza de arrastra sufría una caída brusca. Eiffel no pudo explicar este fenómeno conocido como la crisis del arrastre.
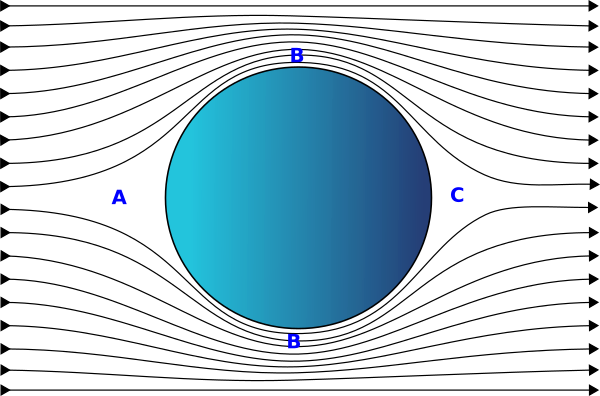
Bola lenta
Antes de ver como se resolvió la crisis del arrastre analicemos una situación más simple, el movimiento de una bola a velocidades bajas que se mueve con flujo laminar.
En el punto A de la imagen donde el aire se encuentra con la bola, su velocidad se reduce aumentando su presión. Al desplazarse por los laterales, B, su velocidad aumenta y disminuye su presión y al llegar a la parte posterior, C, de nuevo aumenta su presión y su velocidad disminuye.
A diferencia de lo que sucede en el flujo turbulento las fuerzas de presión se contrarrestan y la bola solo pierde energía debido a las fuerza de arrastre debidas a la viscosidad del aire.
Si la presión es menor en B que en C, ¿por qué el aire se mueve de B a C y no al revés?
El aire se mueve por inercia en contra de las fuerzas de presión de la misma manera que si lanzamos un objeto hacia arriba se mueve en contra de la fuerza de gravedad.
La Capa Límite
La solución de la crisis del arrastre llegó de la mano de Ludwig Prandtl(1875-1953) y su idea de capa límite.
Cuando una bola se mueve en el aire hay una pequeña zona en torno a la misma, la capa límite, en la que el aire, bajo el dominio de las fuerzas de viscosidad, tiene un flujo laminar hasta números de Reynolds muy elevados en torno a 100000. A partir de este valor el flujo en la capa límite es turbulento.
Bola rápida
Cuando la velocidad de la bola aumenta llega un momento en el que el flujo se vuelve turbulento. Al fluir el aire por los costados de la bola hacia su parte posterior hay una diferencia entre el aire un poco alejado de la bola que se mueve con velocidad elevada y llega fácilmente a la parte posterior y el aire en la capa límite que se mueve lentamente llegando a pararse y a invertir su velocidad al llegar a la parte trasera. Esta inversión da lugar a una estela con remolinos que hace que la presión no vuelva a subir, como sucedía en el flujo laminar, y se produzca una fuerza de arrastre debida a esa diferencia de presión.

Cuando el número de Reynolds supera el valor de 2000 comienza a observarse la estela con remolinos y la fuerzas de presión que estos producen son los que dominan el flujo.
La crisis del arrastre explicada
Cuando la velocidad de la bola alcanza valores muy altos, número de Reynolds mayor que 100000, las fuerzas de presión que frenan la bola sufren una fuerte caída, la crisis del arrastre.
La explicación reside en que la capa límite se vuelve turbulenta. Esta turbulencia aísla las zonas inferiores de la capa límite del flujo principal que continua su camino hacia la parte posterior de la bola. La consecuencia es que la estela turbulenta en la parte posterior queda muy reducida y con ella la fuerza de presión que frena la bola.

Se puede conseguir que la capa límite se vuelva turbulenta para velocidades mucho menores, numero de Reynolds muy inferiores a 100000 haciendo que la bola no sea lisa.
La crisis del arrastre a baja velocidad
Es posible conseguir que la crisis del arrastre se produzca a baja velocidad. Para ello es necesario que el flujo en la capa límite sea turbulento. En el deporte encontramos ejemplos de cómo conseguirlo. Los alvéolos presentes en las bolas de golf o las costuras resultado del cosido de los pentágonos y hexágonos que tienen los balones de futbol hacen que en esos dos deportes la crisis del arrastre tenga lugar a velocidades que se dan en la práctica de ambos. ¿Qué se gana con esa situación?
¿Por qué las bolas de golf tienen alvéolos?
Los primeros jugadores de golf se dieron cuenta de que las bolas nuevas, hechas de gutapercha, tenían un alcance mucho menor que las muy usadas. Estas últimas presentaban una superficie irregular y con pequeñas grietas.
Hoy en día no es necesario esperar a que esto suceda. Los fabricantes de bolas de golf les añaden pequeños alvéolos que consiguen el mismo efecto.
Los alvéolos son los responsable de que la crisis del arrastre tenga lugar a velocidades muy bajas. Esto se traduce en unos alcances mucho mayores. Si al golpear una bola lisa se consigue una distancia de 65 m, usando una con alvéolos se puede llegar a los 230 m.


¿Por qué los balones de futbol tienen costuras?
En la figura se ve un tipo de balón de fútbol muy popular que tiene forma de icosaedro truncado. Su superficie la forman 12 pentágonos y 20 hexágonos, todos regulares, cosidos.
Los polígonos tienen, 12×5 + 20×6 =180 caras.
Una costura une dos caras. En total 90 costuras.
Las 90 costuras hacen el mismo papel que los alvéolos de las bolas de golf, producir la turbulencia necesaria para adelantar la crisis del arrastre. Con un balón de este tipo la crisis del arrastre se produce en torno a los 12 m/s, una velocidad que se consigue fácilmente en el juego. Al diminuir bruscamente la resistencia del aire el balón puede recorrer una distancia mucho mayor a una velocidad elevada. Con un balón liso la crisis del arrastre tendría lugar a unos 37 m/s, velocidad difícilmente alcanzable en el juego. Con los balones lisos las distancias recorridas por el balón serían más pequeñas y el juego mucho más aburrido.

Si olvidamos su curvatura, la forma del balón es un icosaedro truncado, uno de los 13 sólidos de Arquímedes.
La fórmula de Euler relaciona los Vértices, Caras y Aristas de un poliedro:
C + V − A = 2
¿Se cumple aquí?
Efecto Magnus
Cuando lanzamos un objeto en el aire normalmente sigue una trayectoria parabólica debido a la fuerza que la Tierra hace sobre él, su peso. Sin embargo, en muchos deportes en los que se juega con pelotas o bolas como futbol, béisbol o golf, se observan a menudo extrañas trayectorias rectas o curvas muy diferentes de las parábolas verticales habituales. Ejemplos de lo anterior son los goles marcados en un partido de futbol directamente en un saque de esquina, los lanzamientos de bolas curvas o rectas en béisbol, o los golpes en golf en los que la bola describe trayectorias muy distintas de las parábolas esperadas.
Directamente relacionado con lo anterior es la existencia de barcos que han reemplazado sus velas por cilindros giratorios como los que se ven en la foto contigua.


[Imagen de la Biblioteca del Congreso de EEUU]
La causa de todo estos extraños comportamientos es el Efecto Magnus:
Cuando un objeto, que se mueve en un fluido, gira sobre si mismo aparece sobre él una fuerza perpendicular al eje de giro.
[Si el eje de giro no coincide con la dirección del movimiento]
El nombre es en honor del físico alemán Heinrich Gustav Magnus(1802-1870) que lo estudió a mediados del S XIX. El efecto ya era conocido desde hacía mucho tiempo. El inglés Benjamin Robins(1707-1751) lo estudió en 1742 en su relación con proyectiles disparados por armas de fuego. En 1672 la Royal Society publica una carta de Isaac Newton(1641-1727) en la que escribe acerca de la refracción que experimenta la luz al atravesar un prisma. En ella hace referencia al efecto Magnus : «… a menudo he visto que una pelota de tenis golpeada con una raqueta oblicua describe una linea curva»
¿Cuál es la causa del efecto Magnus?
Cuando una bola gira al desplazarse en un fluido aparece sobre ella una fuerza perpendicular al eje de giro.
Cuando el régimen es laminar la situación es parecida a la ya analizada más arriba salvo que ahora el giro de la bola produce una diferencia de velocidades del aire en la parte superior e inferior de la misma. Esa diferencia de velocidades trae consigo una diferencia de presiones que es la que produce la fuerza lateral.
Con frecuencia cuando aparece el efecto Magnus, el régimen es turbulento. En esta situación se produce una estela con remolinos en la parte posterior de la bola. Si la bola no gira, como ya se ha visto, la separación del flujo que forma la estela es simétrica. Sin embargo el arrastre del aire cuando la bola gira produce una asimetría en la separación del flujo. La bola desvía la estela hacia abajo y por tanto ella está sometida a una fuerza deflectora en sentido opuesto. Aunque también existe la diferencia de presiones mencionada en el régimen laminar, la reacción de la estela es la fuerza principal en el régimen turbulento.
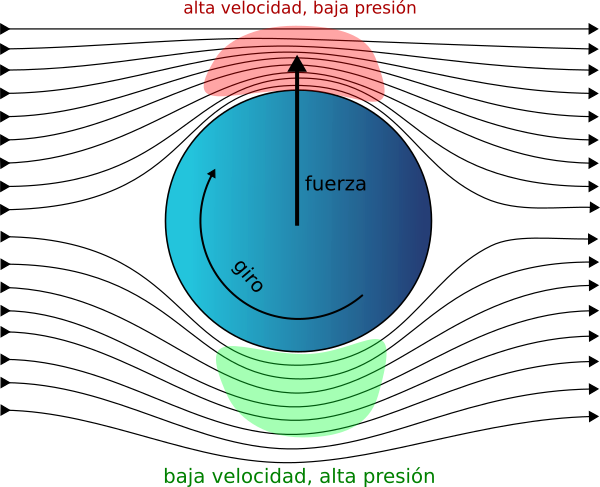
Régimen Laminar
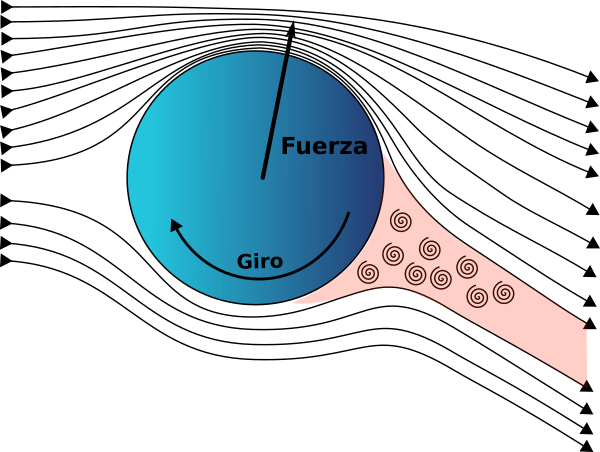
Régimen Turbulento

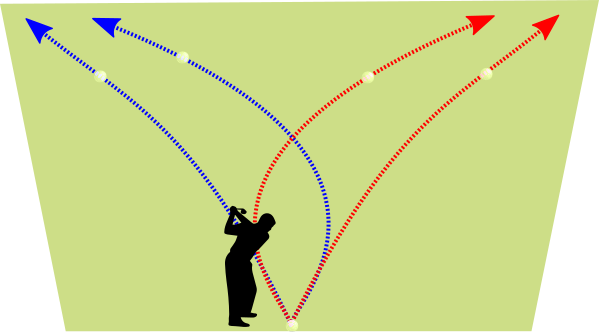
¿Cómo se puede conseguir un tiro curvo en fútbol?
Para conseguir que el balón siga la trayectoria de la imagen, el futbolista tiene que imprimirle con su disparo un giro en sentido antihorario visto desde arriba. Como resultado del efecto Magnus sobre el balón, aparece una fuerza hacia la izquierda que curva su trayectoria.

¿Cómo es posible que una vez golpeada una bola de golf gire a izquierda o derecha o se desplace en línea recta?
Como en la pregunta anterior, para conseguir que aparezca una fuerza lateral sobre la bola, que curve su trayectoria a izquierda o derecha, como consecuencia del efecto Magnus, la bola tiene que girar alrededor de un eje de giro vertical. Por ejemplo para conseguir que la trayectoria de la bola se desvíe hacia la derecha el giro visto desde arriba tiene que tener un sentido antihorario.
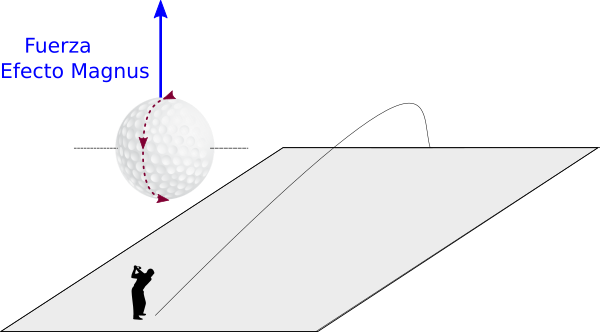
Si la bola gira alrededor de un eje horizontal, la fuerza del efecto Magnus será vertical. Con el sentido de giro adecuado se puede conseguir que la fuerza contrarreste al peso, consiguiendo con ello un alcance mayor.
¿Cómo se puede lanzar en béisbol una pelota recta o curva?
De la misma forma que en las dos preguntas anteriores. El lanzador tiene que imprimir un giro adecuado a la pelota para que, como consecuencia del efecto Magnus, aparezcan fuerzas laterales o verticales que la hagan curvarse o neutralicen el peso de la misma.
¿Por que hay barcos que en lugar de velas tienen cilindros rotatorios?
Debido al efecto Magnus, sobre los cilindros rotatorios aparece una fuerza perpendicular a su eje.
El ingeniero alemán Anton Flettner (1885-1961) ayudado entre otros por el ya mencionado Ludwig Prandtl fue el primero en construir en 1924 un barco que utilizaba este sistema.
En los últimos años ha aumentado el interés por este sistema de propulsión.
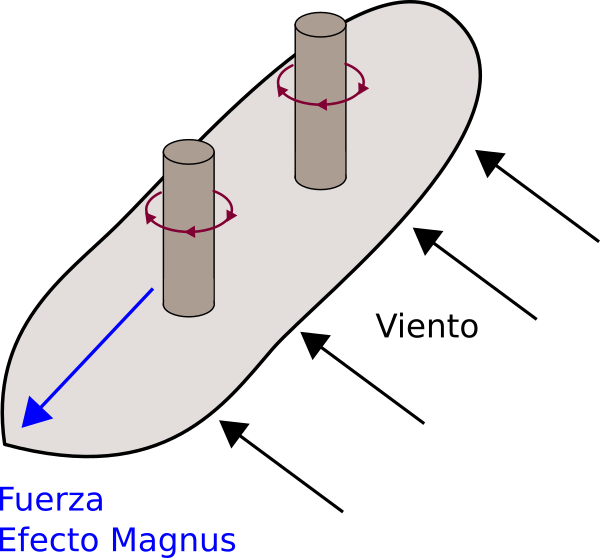
Si los cilindros giran en sentido contrario, la fuerza invierte su sentido.
Ecuaciones de Navier-Stokes
En el estudio de la dinámica de fluidos se utilizan, como hemos visto, los mismos principios y leyes conocidos desde hace varios siglos. Sin embargo su complejidad es tal que incluso el estudio de situaciones descritas por ecuaciones conocidas desde hace más de 100 años presenta dificultades en muchos casos.
Las ecuaciones de Navier-Stokes son un conjunto de ecuaciones diferenciales no lineales en derivadas parciales, nombradas en honor al físico e ingeniero Claude Navier (1785–1836) y al físico y matemático George Stokes (1819-1903). Describen el movimiento de los fluidos tanto para flujos laminares como turbulentos. A día de hoy solo se pueden resolver de forma exacta para ciertos casos particulares que normalmente se corresponden con flujos laminares. A pesar de esta limitación, las ecuaciones de Navier-Stokes constituyen la base para el estudio de comportamiento de los fluidos en todo tipo de situaciones.
El problema de encontrar una solución a las ecuaciones de Navier-Stokes constituye uno de los Problemas del Milenio. El Instituto Clay de Matemáticas en el año 2000 seleccionó siete problemas y estableció un premio de 1 millón de dólares para quien solucionase cualquiera de los siete. El único resuelto hasta la fecha es el de la Conjetura de Poincaré. Fue resuelto por el matemático Grigori Perelman, que renunció al premio por no habérselo ofrecido también a Richard S. Hamilton, sobre cuyo trabajo Perelman basó su solución.
La Hipótesis de Riemann, a día de hoy sin demostrar y de la que ya se ha hablado en estas páginas es quizá el más famoso problema de la lista.
Para saber más
Halliday D., Resnick R., Walker J.1997.Fundamentals of Physics Extended. John Wiley.
[Excelente libro de Física General, tanto por su edición como por su contenido. Halliday y Resnick lo publicaron en 1960. Ha tenido varias ediciones, alguna en español en el siglo pasado. Después del fallecimiento de David Halliday y Robert Resnick, Jearl Walker continua revisándolo y editándolo.]
Bloomfield L. A. 1996. How Things Work. The Physics of Everiday Life. John Wiley.
[Bloomfield consigue llegar al fondo de conceptos y leyes físicas, a través de los objetos que nos rodean, sin utilizar matemáticas]
Walker, J. 2007. The Flying Circus of Physics. John Wiley.
[A través de cientos de preguntas y respuestas Jearl Walker explora los conceptos y leyes físicas que están detrás de lo que hacemos y observamos en nuestra vida cotidiana. La web http://www.flyingcircusofphysics.com/ del libro contiene mucha información interesante]
Arregui De La Cruz, F.; Cabrera Rochera, E.; Cobacho Jordán, R.; Soriano Olivares, J.; Gómez Sellés, E. (2017). Apuntes de mecánica de fluidos. Editorial Universitat Politècnica de València. http://hdl.handle.net/10251/78258
[Se puede descargar libremente desde la página de la Universidad Politécnica de Valencia. Aunque su nivel es universitario y una gran parte requiere poseer conocimientos de cálculo, hay contenido interesante sobre los fluidos y su comportamiento que cualquiera interesado puede apreciar]
Bray, K. (21 de octubre de 2022). A fly walks round a football. https://plus.maths.org/content/comment/2787
[Los balones de fútbol y la crisis del arrastre]
Wesson, J. 2009. The Science of Golf. Oxford University Press.
[El golf visto con los ojos de la Ciencia. Dedica varios capítulos a la física del vuelo de la bola]
