El experimento
Material necesario
- 1 toroide de ferrita (valen muchos tipos)
- 1 resistencia 1 kΩ (vale de 0,5 kΩ a 2 kΩ)
- Unos cuantos ledes de distintos colores.
- 1 transistor PN2222A (hay muchas alternativas posibles)
- Cables para las conexiones y para el bobinado sobre el toroide de ferrita.
- 1 pila AA o AAA de 1,5 V gastada y otra sin gastar para el control.
- 1 placa de pruebas (u otra forma alternativa de hacer las conexiones)

¿Cómo se hace?
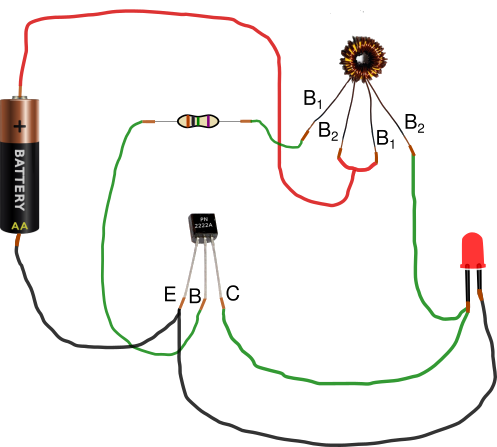
A tener en cuenta

- En el toroide hay dos bobinas superpuestas. Para crear las bobinas se usa hilo de cobre esmaltado, como el que se ve en la fotografía del material, o hilo forrado. Para un toroide como el de la foto hacen falta dos trozos de 50 cm. Una vez bobinados, si se usa hilo de cobre esmaltado, hay que lijar los extremos para eliminar el esmalte

- Las dimensiones aproximadas del toroide utilizado son: diámetro exterior 13 mm, diámetro interior 7 mm y altura 5 mm.
- Un portapilas o unos cables con imanes en los extremos facilitan la conexión de la pila.
- Si se usa un transistor pnp hay que invertir la polaridad de pila y led.
- Los ledes están conectados en serie.
¿Qué sucede?
Si un dispositivo alimentado por pilas deja de funcionar debido a que las pilas están gastadas no significa que estas no tengan todavía energía disponible, lo que suele significar es que la tensión que suministran las pilas ha bajado de un cierto límite que el dispositivo necesita.
El ladrón de julios es un circuito oscilante que funciona como amplificador de tensión. Transforma una tensión continua pequeña en una serie de pulsos de alta frecuencia a una tensión mayor. Consigue así aprovechar mucha energía de una pila aparentemente sin ella.
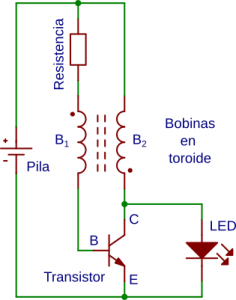
En la figura se representa el esquema de un ladrón de julios.
En una parte del ciclo la energía de la pila se almacena en la bobina B2. En esta parte del ciclo el led está apagado. En la otra parte del ciclo la energía almacenada en la bobina B2 se disipa a través del led encendiéndolo. El transistor actúa como conmutador dando lugar a la oscilación del circuito. [En el dibujo del circuito y en el video la resistencia está entre la bobina B1 y la base mientras que en el esquema está entre B1 y la pila. Ambos circuitos son equivalentes]
Entrando un poco más en detalle:
-
- Inicialmente el transistor está en corte (al no haber corriente de base, se comporta como un interruptor abierto), no circula corriente entre colector y emisor.
- La pila hace que comience a pasar una pequeña corriente a través de la resistencia que, después de atravesar la bobina B1, llega a la base activando el transistor y permitiendo el paso de corriente entre colector y emisor.
- A medida que la corriente aumenta en la bobina B2, se induce corriente en la bobina B1 que refuerza la corriente de base abriendo más el paso a la corriente colector-emisor.
- El paso 3 se repite hasta que el transistor está en saturación y la corriente que atraviesa la bobina 2 y el canal colector-emisor ha llegado al máximo. En este momento hay una gran energía almacenada en el campo magnético de la bobina B2.
- Como la corriente no varía en la bobina B2, desaparece el efecto de inducción sobre la bobina 1 y comienza a descender la corriente que llega a la base.
- Al disminuir la corriente de base, el canal colector-emisor comienza a cerrarse produciendo una disminución de corriente en la bobina B2.
- La caída de corriente en la bobina B2 provoca que en la bobina B1 la corriente disminuya también.
- La repetición de los pasos 6 y 7 pone al transistor en corte.
- Con el transistor en corte, la energía magnética que queda almacenada en la bobina B2 provoca un pulso de corriente a través del led.
- Una vez que la energía de la bobina se ha disipado, todo comienza de nuevo.
Los puntos que aparecen en el símbolo de las bobinas en el esquema del circuito, indican puntos con misma polaridad instantánea.
En un ladrón de julios típico la frecuencia de funcionamiento es del orden de 50 kHz mientras que la tensión de salida puede estar en torno a los 30 V.
Un poco de historia
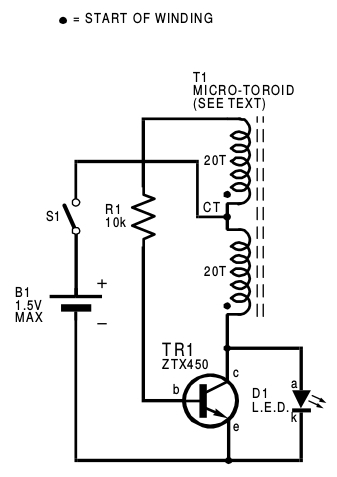
En el número de noviembre de 1999 la revista Everyday Practical Electronics publicó un articulo firmado por Z. Kaparnik con el título One Volt LED-A Bright Light. Presentaba tres circuitos que permitían encender un led con una fuente de tensión mucho menor que la necesaria para encenderlo directamente. El circuito más simple de los tres presentados es el que aparece en la figura.
En palabras de Kaparnik:
In the Micro-torch circuit Fig.1a, transistor TR1, transformer T1 and resistor R1 form a current-controlled switching oscillator. Each time TR1 turns off, the collapsing magnetic field in T1 generates a 30V (off-load) positive pulse at TR1’s collector (c). This, in series with the supply, is fed directly to the LED.
Switching occurs at a very high frequency and with a low duty cycle, which results in an average LED current of about 18mA, sufficient to illuminate most LEDs.
Más información
- Joule thief en wikipedia: https://en.wikipedia.org/wiki/Joule_thief
- Make a Joule Thief for Zombie Batteries: https://youtu.be/B61DU7yEsPM
- How a Joule Thief Works: https://youtu.be/0GVLnyTdqkg
- Ladron de Joules con Transistor PNP: https://www.taringa.net/posts/hazlo-tu-mismo/18538702/Ladron-de-Joules-con-Transistor-PNP.html
Créditos
- ¿Qué sucede? está adaptado de http://www.instructables.com/id/Joule-Thief-Low-Voltage-Battery-Charger/
(Licencia: Attribution-NonCommercial-ShareAlike 2.5 Generic (CC BY-NC-SA 2.5) ) - La figura 1a está adaptada de http://www.instructables.com/id/How-to-Make-a-Joule-Thief-Boost-Converter/
(Licencia: Attribution-NonCommercial-ShareAlike 2.5 Generic (CC BY-NC-SA 2.5) ) - El esquema del circuito en la figura 2 está adaptado de https://commons.wikimedia.org/wiki/File:Joule_thief_schematic_de.svg (Licencia: Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0)
