Una hormiga viajera
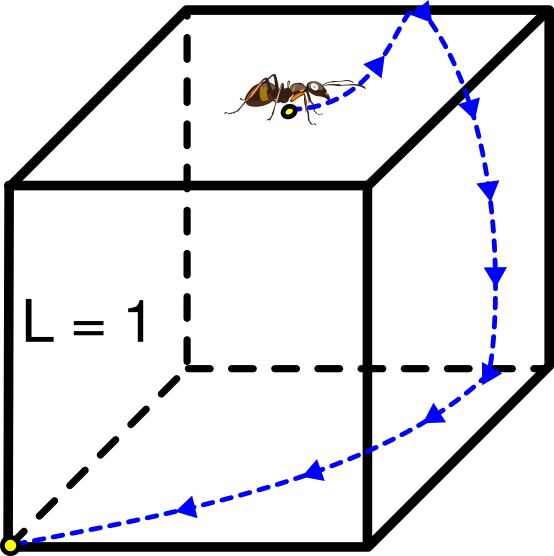
Una hormiga que está en el centro de la cara superior de un cubo quiere ir a un vértice de la cara inferior como se ve en la figura. Si la arista del cubo mide L = 1 ¿qué distancia mínima debe recorrer?
Una serie infinita
En un triángulo equilátero de lado L = 1 se inscribe una sucesión infinita de círculos, cada uno sobre el anterior, como se ve en la figura
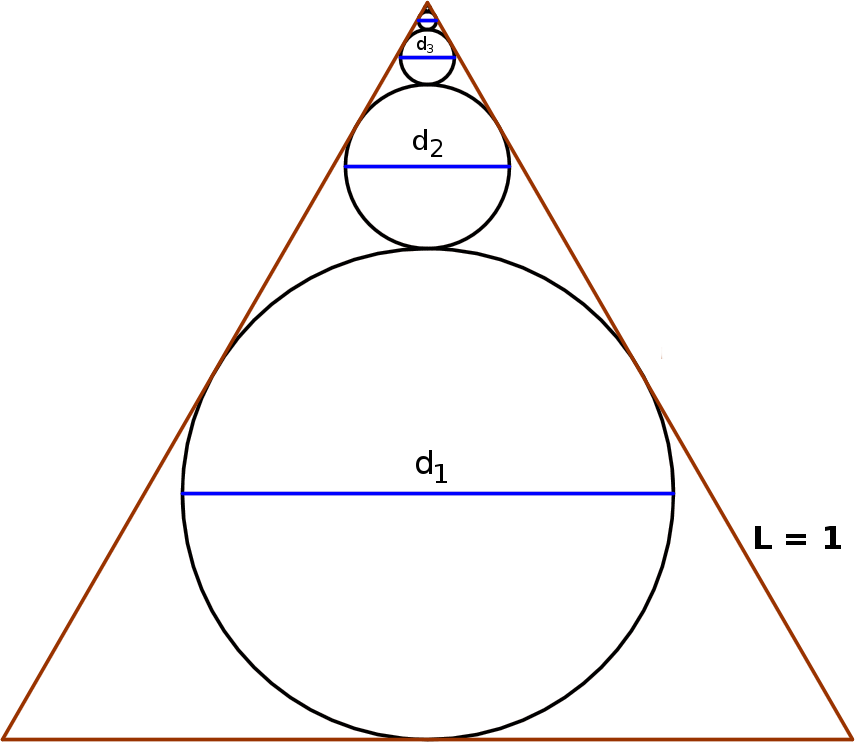
¿Cuanto vale la suma de los diámetros de todos los círculos?
Geometría euclídea
En un cuadrante de circunferencia hay inscrito un rectángulo como se ve en la figura
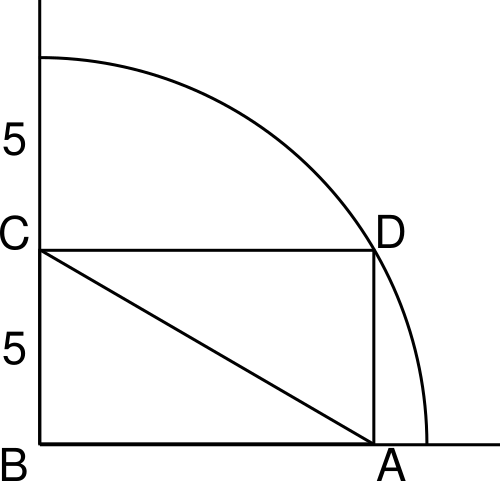
Determina la longitud de la diagonal AC
*Tiempo límite para resolver los 3 rompecabezas = 5 minutos
ver soluciones
