¿Puede haber belleza en las matemáticas?
Si se hiciese una encuesta con esta pregunta y otras similares en relación con otras actividades humanas, la mayoría de los encuestados no tendría inconveniente en admitir que puede haber belleza en un cuadro de Pablo Picasso o en un lied de Franz Schubert, pero pocos estarían dispuestos a hablar de belleza en relación con las matemáticas, la física u otras ciencias naturales.

Un grupo de investigadores británicos dirigidos por Semir Zeki, con la colaboración de 16 matemáticos, estudiaron, usando resonancia magnética funcional, qué partes del cerebro se activan cuando un matemático ve una formula que previamente ha clasificado como bella, fea o indiferente. Los resultados mostraron que cuando los matemáticos veían ecuaciones que calificaban como bellas, se activaban las mismas áreas cerebrales que cuando se experimenta belleza de una fuente más convencional como la contemplación de un cuadro.
Resulta interesante ver las distintas valoraciones que hacen los matemáticos participantes sobre la belleza de las 60 fórmulas presentadas. Por cierto, la fórmula más valorada fue la identidad de Euler,
Algunas opiniones
Es fácil encontrar, entre los profesionales, opiniones apasionadas sobre el tema:

Para Paul Dirac, uno de los padres de la mecánica cuántica, la belleza matemática fue una guía en su carrera. En un artículo publicado en Scientific American en mayo de 1963 comparaba la forma en que Erwin Schrodinger y Werner Heisenberg sentaron las bases de la mecánica cuántica al explicar el comportamiento observado del átomo de hidrógeno. Schrödinger utilizó su famosa ecuación de onda, que para Dirac describía el átomo de hidrógeno de una forma más intuitiva y bella que la mecánica de matrices, mas abstracta, de Werner Heisenberg. Los dos enfoques explicaban lo observado en el laboratorio. En palabras de Dirac:
"Creo que hay una moraleja en esta historia, es más importante que tus ecuaciones tengan belleza que se ajusten al experimento".
El propio Dirac contribuyó a la descripción del átomo de hidrógeno con la ecuación que lleva su nombre. Al fusionar la mecánica cuántica con la relatividad especial de Einstein conseguía explicar de una forma mucho más completa el comportamiento observado. Su ecuación también implicaba la existencia de la antimateria, posteriormente confirmada,
Cuando le preguntaron a Dirac por su ecuación contestó: «La encuentro hermosa»
Para Bertrand Russel :
“Las matemáticas, justamente consideradas, poseen no sólo la verdad, sino también una belleza suprema, una belleza fría y austera, como la de la escultura, sin apelar a ninguna parte de nuestra débil naturaleza, sin los hermosos adornos de la pintura o la música, pero sublimemente pura y capaz de una perfección severa como solo el arte más grande puede mostrar " [Misticismo y lógica y otros ensayos]
G. H. Hardy también se interesó por el tema. En su libro A Mathematician’s Apology, no solo deja claro que las matemáticas tiene que ser bellas:
"Los patrones del matemático, como los del pintor o el poeta deben ser hermosos; las ideas como los colores o las palabras, deben encajar de una manera armoniosa. La belleza es la primera prueba: no hay lugar permanente en el mundo para las matemáticas feas"
sino que también establece criterios para que las demostraciones lo sean.
Masahiko Fujiwara en las conversaciones que mantiene con Yoko Ogawa en Introducción a la belleza de las matemáticas:
"La matemática, al menos originalmente, no proporciona beneficio alguno. No digo que no pueda encontrársele alguna aplicación práctica de aquí a 500 años, pero en el momento en que se hace un descubrimiento matemático es difícil ver que pueda dársele alguna utilidad. Así pues, ¿qué valor tiene? La respuesta es solo una: su valor depende de su belleza. Y por eso es de suma importancia para un matemático haber contado con una educación estética"
Martin Gardner, además de divulgador de las matemáticas, fue matemago . En Mathematics, Magic and Mystery:
La matemagia combina la belleza de la estructura matemática con el valor de la diversión que produce un truco.
¿Dónde buscar la belleza de las matemáticas?
El matemático húngaro Paul Erdős decía que las demostraciones más bellas están en El Libro, en el que Dios guarda las demostraciones perfectas de los teoremas matemáticos. Erdős, que no era creyente, añadía, «no necesitas creer en Dios, pero, como matemático si debes creer en El Libro». En los últimos años de su vida colaboró con los matemáticos Martin Aigner y Günter M. Ziegler que estaban escribiendo una versión de El Libro. Erdős falleció en 1996, 2 años antes de la publicación de: Proofs from The Book. En 2018 se ha publicado la sexta edición.
François Le Lionnais cofundador con Raymond Queneau del grupo OULIPO, en La Beauté en Mathématiques propone buscar la belleza en los hechos y en los métodos que las matemáticas proporcionan. Sugiere que como con las obras de arte, podemos abordar las belleza de las matemáticas desde el clasicismo, todo sobriedad elegante y desde el romanticismo, deleite con efectos sorprendentes encaminados al paroxismo.
Algunos lugares donde buscar la belleza de las matemáticas:
-
- Las demostraciones y las técnicas de resolución de problemas
- Los teoremas y ecuaciones
- Los objetos matemáticos y sus representaciones.
Y por supuesto haciendo matemáticas. No es necesario ser un profesional para poder disfrutar de hacer matemáticas a muchos niveles. George M. Phillips en Mathematics Is Not a Spectator Sport nos anima a hacer matemáticas ya que, a diferencia de lo que sucede en música, en la que hay músicos activos, que cantan o tocan un instrumento, y músicos pasivos que escuchan lo que producen los primeros, mantiene que solo hay un tipo de matemáticos: los activos. No hay matemáticos pasivos.
¿Qué características de las matemáticas las hacen bellas?
G.H. Hardy en su A Mathematician’s Apology dice que para poder apreciar belleza en una demostración, ha de ser general, profunda, inesperada, inevitable, económica y seria.
Al hablar de la belleza de una demostración o de una técnica matemática se suelen exigir ciertas condiciones. Son frecuentes las siguientes:
-
- Elegancia, simplicidad, brevedad
- Relevancia matemática, profundidad, generalidad
- Factor sorpresa
- Interconexión con otras ramas matemáticas
A continuación se presentan algunos demostraciones y técnicas en las que se dan algunas de estas condiciones.
Un clásico: 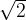 es un número irracional
es un número irracional
(Un número es irracional si no se puede expresar en forma de una fracción de dos números enteros)
Este hecho, de gran trascendencia en la historia de las matemáticas, fue un descubrimiento de la Escuela Pitagórica. La demostración que sigue, utiliza el método de Reducción al Absurdo. Se empieza por suponer como cierto lo contrario de lo que se quiere demostrar. Si al hacerlo se llega a una contradicción, se puede deducir que lo que se quería demostrar originalmente era cierto.
Demostrar que es un número irracional
Supongamos que no lo es. Si es un número racional se puede expresar como el cociente de dos números enteros a y b. Supongamos también que a y b están en su forma irreducible, no tienen factores comunes.
Ahora elucubremos tratando de encontrar una contradicción.
Al elevar al cuadrado la expresión anterior,
se obtiene,
De esta expresión se deduce que a es un número par y se puede escribir,
Siendo c un número entero. Al substituir en la expresión anterior,
O lo que es lo mismo,
Esto implica que b también es un número par. Inicialmente se había supuesto que a y b no tenían factores comunes. Como se ha llegado a una contradicción, se puede deducir que la suposición inicial es falsa y consecuentemente es un número irracional.
Intermedio entre dos clásicos: Un demostración divertida
Teorema: Existen 2 números irracionales a, b tales que ab es un número racional.
Demostración:
Si ,
una de las siguientes afirmaciones,
tiene que ser verdadera, ya que la segunda es la negación de la primera.
Si es la primera, el teorema ya está demostrado.
Si es la segunda,
también está demostrado.
Aunque hemos demostrado el teorema, no sabemos cual de las dos afirmaciones es la cierta. Si tenemos curiosidad podemos acudir al teorema de Gelfond–Schneider: la segunda afirmación es la verdadera.
Otro clásico: La secuencia de los números primos no tiene fin

La prueba que aquí se presenta se atribuye a Euclides. Es la proposición 20 del libro IX de los Elementos. También utiliza el método Reducción al Absurdo.
Empezamos afirmando lo contrario de lo que queremos demostrar:
El número de primos es finito. Hay n:
Cualquier número que no está en esta lista es por tanto compuesto y se puede dividir por uno de los n primos. Como en la demostración anterior, se intentará buscar un hecho que contradiga el que se ha establecido como cierto.
Consideremos el siguiente número,
m es mayor que el último primo y además no es compuesto ya que al dividirlo por cualquiera de los n primos,
da de resto 1.
Por tanto o bien m es primo o es divisible por un primo mayor que . Esto contradice la afirmación inicial, por tanto:
La secuencia de los números primos no tiene fin
y otro más. La Diagonal de Cantor

La tercera demostración clásica, con un lugar merecido en El Libro, se debe al matemático alemán Georg Cantor. Tiene su lugar en la historia de las matemáticas por poner en evidencia que no todos los infinitos son iguales.
Antes de entrar en la demostración revisemos algunos conocimientos básicos sobre conjuntos.
Un conjunto es un grupo de elementos que comparten alguna característica común. Por ejemplo, el conjunto de las vocales del alfabeto español {a,e,i,o,u} o el conjunto de los números primos entre 10 y 20 {11, 13, 17, 19}.
La cardinalidad de un conjunto es el número de elementos que contiene. La cardinalidad del conjunto {a,e,i,o,u} es 5 mientras que la de {11, 13, 17, 19} es 4.
Además de conjuntos finitos como los anteriores hay conjuntos infinitos como por ejemplo, el conjunto de los números naturales N = {1, 2, 3, … }, el conjunto de los números impares {1, 3, 5, …} o el conjunto de los múltiplos de 27 {27, 54, 81, …}.
Cantor hizo notar que también tiene sentido hablar de cardinalidad de un conjunto infinito.
Definió la cardinalidad del conjunto de los números naturales como el número álef cero, ℵ0.
Si un conjunto se puede emparejar elemento a elemento con el conjunto de los números naturales, se le denomina numerable y tiene el mismo número de elementos, la misma cardinalidad, ℵ0, que el conjunto de los naturales, N.
El párrafo anterior es una extensión natural a lo que hacemos cuando contamos el número de elementos de un conjunto finito. Para determinar la cardinalidad del conjunto de las vocales, emparejamos sus elementos con los del conjunto de los 5 primeros números naturales.
Aunque la forma de contar conjuntos finitos e infinitos sea similar, cuando determinamos la cardinalidad de un conjunto infinito podemos llevarnos alguna sorpresa.
El conjunto de los números impares es numerable ya que es posible emparejarlo 1 a 1 con N
1, 3, 5, 7, 9, 11, 13, …
↓ ↓ ↓ ↓ ↓ ↓ ↓, …
1, 2, 3, 4, 5, 6, 7, …
El conjunto de los naturales y el conjunto de los impares tienen por tanto, y sorprendentemente, el mismo número de elementos, ℵ0.
De forma análoga se puede comprobar que son numerables, tienen la misma cardinalidad, el conjunto de los múltiplos de 27, el conjunto de los números enteros {…, -3, -2, -1, 0, 1, 2, 3, …}, o el conjunto de los números racionales (todas las fracciones cuyo numerador y denominador son números enteros)
Llegados a este punto surge la pregunta ¿son todos los conjuntos infinitos numerables? o la equivalente ¿tienen todos el mismo número de elementos?
La respuesta la dio Cantor al demostrar que el conjunto de los números reales no es numerable.
Utilizó en su demostración el método de Reducción al Absurdo:
Supongamos que el conjunto de los números reales es numerable. Si es así, es posible hacer una lista emparejando cada número natural con un número real,
1 ← e1,d11d12d13d14d15d16d17…
2 ← e2,d21d22d23d24d25d26d27…
3 ← e3,d31d32d33d34d35d36d37…
4 ← e4,d41d42d43d44d45d46d47…
5 ← e5,d51d52d53d54d55d56d57…
6 ← e6,d61d62d63d64d65d66d67…
A la derecha de la coma se representa los dígitos de la parte decimal de cada número real.
La clave de la demostración reside en que es posible encontrar un numero real que no está en la lista que supuestamente los contiene a todos. Se puede construir de la siguiente manera:
se escoge como su primera cifra decimal una diferente de d11,
se escoge como su segunda cifra decimal una diferente de d22,
se escoge como su segunda cifra decimal una diferente de d33,
se escoge como su segunda cifra decimal una diferente de d44,
se escoge como su segunda cifra decimal una diferente de d55,
se escoge como su segunda cifra decimal una diferente de d66,
y así sucesivamente. La parte entera del número elegido puede ser cualquiera.
El número así construido no está en la lista ya que se diferencia de cada uno de los de la lista en al menos un decimal. Como esto contradice la afirmación inicial, podemos concluir que:
El conjunto de los números reales no es numerable. Tiene más elementos que el conjunto de los naturales.
Su cardinalidad se representa por la letra c, la inicial de continuo, otro nombre para el conjunto de los reales.
Cantor intento, durante muchos años sin conseguirlo, demostrar lo que se conoce como la hipótesis del continuo:
No hay conjuntos cuya cardinalidad esté comprendida entre la de los naturales, ℵ0, y la de los reales, c.
David Hilbert la incluyó en 1900 en su famosa lista de problemas sin resolver. A la muerte de Cantor en 1918 seguía sin demostrase.
Los trabajos de Kurt Gödel en 1940 y Paul Cohen en 1963 dieron solución al problema, ¿o no?
Kurt Gödel demostró en 1940 que la existencia de un conjunto con cardinalidad intermedia no se podía demostrar dentro de la teoría de conjuntos estándar. Paul Cohen en 1963 demostró que, dentro de la teoría de conjuntos estándar, tampoco se podía demostrar la no existencia de un conjunto con cardinalidad intermedia.
El fideo de Buffon

En 1777 Georges Louis Leclerc, Conde de Buffon, propuso el siguiente problema, conocido popularmente como La Aguja de Buffon:
Si se lanza una aguja de longitud L sobre un suelo en el que hay dibujadas lineas equidistantes una distancia D (≥L), ¿cuál es la probabilidad de que la aguja corte a una linea? (ver la entrada: ¿Qué tiene que ver el número pi con el número de supervivientes?)
El propio Buffon calculó la probabilidad solicitada haciendo uso del cálculo infinitesimal. La probabilidad de corte es,
En Havil [2007] puede verse la solución del problema planteado y también la solución para el caso L > D.

En 1860 Joseph-Émile Barbier propuso una solución que sin resolver ninguna integral permite contestar a la pregunta de Buffon de una forma elegante. En lugar de preguntarse ¿cual es la probabilidad de que la aguja corte una línea? se preguntó ¿cuál es el número de cortes que se producirán en promedio? A diferencia de la probabilidad, el promedio de cortes varía linealmente con la longitud de la aguja y esto es así aunque doblemos la aguja en forma de V, en forma de polígono o de una figura más compleja como un fideo, de ahí el nombre, con la condición de que la figura sea plana. Llamando N al promedio de cortes, L a la longitud del fideo y c a la constante de proporcionalidad, la relación es,
La clave de la solución es utilizar un fideo circular con una longitud = πD. Siendo D la separación entre las lineas del suelo.
En este caso, resulta evidente que la aguja circular cortará siempre 2 líneas. Por tanto,
y el promedio de cortes,
Para la pregunta de Buffon en la que D ≥ L el promedio de cortes coincide con la probabilidad buscada.
Si en lugar de la circunferencia utilizamos una curva de ancho constante, D, el resultado también sería el mismo. Barbier enunció el siguiente teorema que lleva su nombre: Todas las curvas de ancho constante D tienen un perímetro πD, esto implica que el fideo no necesariamente tiene que tener forma circular sino que puede tener la forma de cualquier curva de ancho constante D. (Ver la entrada: Triángulos de Reuleaux y otras curvas de ancho constante)
Una descripción intuitiva y muy asequible en Stein [2001]. Otra más rigurosa: Aigner y Ziegler[2002]
Métodos elegantes de solución de problemas
Tres retos para terminar. Las soluciones que se muestran utilizan técnicas que, por su elegancia, economía de recursos o la sorpresa que causan, son un ejemplo de belleza.
Para apreciar mejor las soluciones propuestas es conveniente, antes de verlas, intentar la resolución de cada reto.
Reto nº 1

¿Es posible mover la ficha azul a la casilla inferior derecha del rectángulo cumpliendo las condiciones siguientes?
-
- En cada movimiento la ficha puede pasar a una casilla contigua
- Casillas contiguas son aquellas que comparten un lado
- La ficha ha de pasar por todas las casillas
- La ficha no puede pasar dos veces por la misma casilla
Reto nº 2
Demostrar que en una reunión de 100 personas hay al menos dos que tienen el mismo número de conocidos en el grupo.
Reto nº 3
En la entrada la serie armónica se revisa lo que se entiende en matemáticas por una serie y su suma. Hay series que se pueden sumar (convergentes) y otras que no es posible sumar (divergentes), su suma no tiene límite, crece indefinidamente. El comprobar si una serie es convergente no es siempre es tarea sencilla y la búsqueda de criterios para determinar este hecho es una de la tareas a las que se dedica el análisis.
La serie armónica:
,
es divergente, su suma no tiene límite. En 1350 Nicolas de Oresme lo demostró de una manera elegante, haciendo uso de matemáticas elementales.
En esto consiste este tercer reto, demostrar que la serie armónica es divergente.
Para saber más
Aigner, M., Ziegler, G.M. 2002. Proofs from The Book. Springer.
Hay edición en español:
Aigner, M., Ziegler, G.M.2005. EL LIBRO de las demostraciones. Nivola
[Una colección de demostraciones que según Paul Erdős deberían estar en El Libro, en el que Dios guarda las demostraciones perfectas de los teoremas matemáticos. Erdős añadía, «no necesitas creer en Dios, pero, como matemático si debes creer en El Libro». Participó en el libro hasta su muerte en 1996.
El capítulo 20, «Buffon’s needle problem», está dedicado básicamente a la forma en que Barbier resolvió el problema de la aguja de Buffon, aunque incluye también la forma de encontrar la probabilidad pedida mediante el cálculo. Para disfrutar de una parte del libro hay que estar acostumbrado al lenguaje matemático formal y conocer las matemáticas que se estudian en los últimos cursos de enseñanza media]
Alsina i Català, C., Nelsen, R. B. 2010. Charming Proofs: A Journey into Elegant Mathematics. Mathematical Association of America.
Hay edición en español:
Alsina i Català, C., Nelsen, R. B. 2021. Demostraciones con encanto: Un viaje por las matemáticas elegantes. Ediciones SM
[Colección de demostraciones sobre números, geometría, desigualdades, funciones, origami, teselaciones, elegantes, sucintas e ingeniosas. Al final de cada capítulo desafíos al lector]
Dunham, W. 1990. Journey Through Genius: The Great Theorems of Mathematics. John Wiley
Hay edición en español:
Dunham, W. 2002. Viaje a Través de los Genios: Biografías y Teoremas de los Grandes Matemáticos. Pirámide
[En los capítulos, 11. La no enumerabilidad del continuum (1874) y 12. Cantor y el reino de lo transfinito (1891), Dunham revisa la incursión de Cantor en el infinito así como la revolución que supuso en las matemáticas de finales del S XIX. De fácil y recomendable lectura, no solo estos dos capítulos sino todo el libro.]
Hardy, G.H. 1940 . A Mathematician’s Apology . Cambridge University Press.
Hay ediciones en español:
Hardy, G.H. 1999. Apología de un matemático. Nivola . Prologo de Miguel de Guzmán
Hardy, G.H. 2017. Apología de un matemático. Capitán Swing. Introducción de José Manuel Sánchez Ron
[Todas las ediciones incluyen una extensa biografía de Hardy escrita por C. P. Snow]
Havil, J. 2007. Nonplussed!. Mathematical Proof of Implausible Ideas. Princeton University Press
[Solución del problema de la aguja de Buffon. Analiza ambos casos L ≤ D y L > D. Son necesarios conocimientos de cálculo infinitesimal ]
Kennedy, J. (2 de mayo de 2022). Can the Continuum Hypothesis Be Solved?.
https://www.ias.edu/ideas/2011/kennedy-continuum-hypothesis
[Más información sobre la Hipótesis del Continuo]
Le Lionnais, F. 1948. La Beauté en Mathématiques. en Les Grands Courants de la pensée mathématique, Cahiers du Sud.
Polster, B. 2004. Q.E.D. Beauty in Mathematical Proof. Walker & Co.
[Colección de demostraciones matemáticas presentadas visualmente]
Stein, S. 2001. Adventures in Mathematical Reasoning. Dover.
[El capítulo 1, The Needle and the Noodle, está dedicado a analizar en detalle el problema conocido como el fideo de Buffon. El libro cumple lo que promete su autor: tratar conceptos de matemática avanzada usando solamente matemáticas básicas y sentido común. Muy Recomendable]
Zeki, S., Romaya, J. P., Benincasa, D. M. T., & Atiyah, M. F., The experience of mathematical beauty and its neural correlates. Frontiers in Human Neuroscience. Front. Hum. Neurosci. 8, 68 (2014) .
[Al artículo le acompañan: la lista de las 60 ecuaciones presentadas, el cuestionario utilizado, una hoja de cálculo con los resultados obtenidos,…]
